Skip to main content
Logo image

Quantitative Wisdom: Numerical literacy from the perspective of Biblical wisdom

Dr. Ryan Johnson

Appendix B Solutions to Odd Exercises

3 Finance
3.1 Introduction to Spreadsheets
3.1.7 Exercises

3.1.7.1.

Solution.
=4/7 which gives approximately 0.571429

3.1.7.3.

Solution.
=8+19 which gives 27

3.1.7.5.

Solution.
=12*9 which gives 108

3.1.7.7.

Solution.
=8^3 which gives 512

3.1.7.9.

Solution.
=7.50/44.50 which gives approximately 0.1685, or approximately 16.85%

3.1.7.11.

Solution.
  1. =5780.23-5250 which gives $530.23
  2. =530.23/5250 which gives approximately 0.100996, or approximately 10.1%
  3. Exactly 200%
  4. =5250*115.5% which gives exactly $6063.75

3.1.7.13.

Solution.
  1. =1000*103%*103% which gives $1060.90
  2. =1000*(103%)^2 gives the same result of $1060.90, because raising 103% to the second power means the same as multiplying 103% by itself two times.
  3. =1000*(103%)^15 which gives $1557.97 rounded to the nearest cent
  4. Refer to the table at the bottom for part d and part e.
    Note the entry in cell B3 here is = B2*103% and the remaining cells are computed using the fill down feature.
    You will have to wait a minimum of 24 full years, in each case, in order for the balance to finally exceed twice the opening deposit amount.
  5. Since \((103\%)^{23} \lt 2 \lt (103\%)^{24}\text{,}\) the minimum number of full years until the opening deposit doubles must be the same here, for any positive opening balance that we may choose for this account.
A portion of a spreadsheet is shown, which includes cells A1 through E32, and with a title heading of Table 3. Cell A1 shows a column title of Year, and cells A2 through A32 contain values of 0 through 30, respectively. Cells D1 through D32 are a copy of cells A1 through A32. Cell B1 shows a column title of Balance. Cell B2 shows $1,000.00, which corresponds to Year 0 displaying in adjacent cell A1. Cell B3 shows $1,030.00, which is 103% of the $1,000 shown in cell B2. Cell B4 shows $1,060.90, which is 103% of the $1,030.00 shown in cell B3. This pattern continues until we get to cell B32, which shows $2,427.26, and which is 103% of the $2,356.57 amount shown in cell B31. Cell E1 shows a column title of Balance. Cell B2 shows $5,000.00, which corresponds to Year 0 displaying in adjacent cell D1. Cell E3 shows $5,150.00, which is 103% of the $5,000 shown in cell E2. Cell E4 shows $5,304.50, which is 103% of the $5,150.00 shown in cell E3. This pattern continues until we get to cell E32, which shows $12,136.31, and which is 103% of the $11,782.83 amount shown in cell E31.

3.2 Simple and Compound Interest
3.2.11 Exercises

3.2.11.1.

Solution.
\begin{align*} A\amp=200+200(0.05)\\ \amp=\$210 \end{align*}
You will have to repay $210.

3.2.11.3.

Solution.
\begin{align*} A\amp=200+200(0.06)(1.25)\\ \amp=\$215 \end{align*}
$215 was repaid.

3.2.11.5.

Solution.
  1. \begin{align*} A\amp=20000+20000(0.05)(10)\\ \amp=\$30,000 \end{align*}
  2. \begin{align*} A\amp=20000(1+0.05)^{10}\\ \amp=\$32,577.89 \end{align*}
The simple interest account would be worth $30,000 and the account that was compounding would be worth $32,577.89 in ten years.

3.2.11.7.

Solution.
\begin{align*} A\amp=1000\left(1+\frac{0.07}{52}\right)^{52*20}\\ \amp\approx \$4051.38 \end{align*}
The account balance is $4,051.38 in 20 years.
Or,
=FV(0.07/52,52*20,0,1000)

3.2.11.9.

Solution.
  1. \begin{align*} A\amp=300\left(1+\frac{0.05}{1}\right)^{1*10}\\ \amp\approx \$488.67 \end{align*}
    There will be $488.67 in the account in 10 years.
    Or,
    =FV(0.05/1,1*10,0,300)
  2. \begin{align*} I\amp=488.67-300\\ \amp=\$188.67 \end{align*}
    $188.67 of the balance will be interest.
  3. \begin{gather*} \frac{188.67}{488.67} \approx 0.3861 \text{ or } 38.61\% \end{gather*}
    The interest makes up 38.61% of the balance.

3.2.11.11.

Solution.
  1. \begin{align*} A\amp=10000\left(1+\frac{0.04}{52}\right)^{52*25}\\ \amp\approx \$27,172.37 \end{align*}
    The balance is $27,172.37.
    Or,
    =FV(0.04/52,52*25,0,10000)
  2. \begin{align*} I\amp=27172.37-10000\\ \amp=\$17,172.37 \end{align*}
    The interest is $17,172.37.
  3. \begin{gather*} \frac{17172.37}{27172.37} \approx 0.632 \rightarrow 63.2\% \end{gather*}
    The percent that is interest is 63.2%.
  4. \begin{gather*} \frac{10000}{27172.37} \approx 0.368 \rightarrow 36.8\% \end{gather*}
    The percentage that is the principal is 36.2%.

3.2.11.13.

Solution.
\begin{align*} P\amp=\frac{20000}{\left(1+\frac{0.05}{4}\right)^{4*4}}\\ \amp\approx \$16,394.79 \end{align*}
The principal required would be $16,394.79
Or,
=PV(0.05/4,4*4,0,20000)

3.2.11.15.

Solution.
  1. Bill =EFFECT(0.0375,12) =3.82% and Ted =EFFECT(0.038,1) =3.8%. Bill has an effective rate of 3.82% and Ted has a rate of 3.8%.
  2. \begin{align*} A\amp=6700\left(1+\frac{0.0375}{12}\right)^{12*5}\\ \amp\approx \$8,079.38 \end{align*}
    Or, =FV(0.0375/12,5*12,0,6700)
    \begin{align*} A\amp=6500\left(1+\frac{0.038}{1}\right)^{1*5}\\ \amp\approx \$7,832.49 \end{align*}
    Or, =FV(0.038,5,0,6500)
    The account balances are $8,079.38 and $7,832.49. So, Bill’s balance is higher.

3.2.11.17.

Solution.
  1. \begin{align*} A\amp=2500e^{0.04*10}\\ \amp\approx \$3,729.56 \end{align*}
    Or, 2500*EXP(0.04*10)
    The account balance is $3,729.56.
  2. \begin{align*} I \amp= 3729.56-2500\\ \amp= \$1229.56 \end{align*}
    The interest earned is $1,229.56.
  3. \begin{gather*} \frac{1229.56}{3729.56} \approx 0.3297 \rightarrow 32.97\% \end{gather*}
    32.97% of the balance is interest.

3.2.11.19.

Solution.
  1. \begin{align*} A\amp= 5000e^{0.045*5}\\ \amp\approx \$6,261.61 \end{align*}
    Or, =5000*EXP(0.045*5)
    The account balance is $6,261.61.
  2. \begin{align*} I \amp= 6261.61-5000\\ \amp= \$1,261.61 \end{align*}
    The interest earned is $1,261.61
  3. \begin{gather*} \frac{1261.61}{6261.61} \approx 0.2015 \rightarrow 20.15\% \end{gather*}
    The interest is 20.15% of the balance.

3.3 Savings Plans
3.3.6 Exercises

3.3.6.1.

Solution.
  1. \(\frac{250[(1+\frac{0.065}{12})^{12*35}-1]}{(\frac{0.065}{12})}\)
    Or, FV(0.065/12,12*35,250)
    In 35 years you will have $400,079.05 in your retirement plan.
  2. \(400079.05 - 12*35*250\text{.}\) You will have earned $295,079.05 in interest.
  3. \(295079.05 /400079.05\text{.}\) The final balance will be about 73.8% interest.

3.3.6.3.

Solution.
  1. \(\frac{750\left(1+\frac{0.0775}{4})^{4*30}-1\right)}{\left(frac{0.0775}{4}\right)}\)
    Or, =FV(0.0775/4,4*30,750)
    In 30 years you will have $348,456.10 in your retirement plan.
  2. \(348456.1 - 4*30*750\text{.}\) You will have earned $258,456.10 in interest.
  3. \(258456.1 /348456.1\text{.}\) The final balance will be about 74.2% interest.

3.3.6.5.

Solution.
  1. In 5 years: \(\frac{130\left(\left(1+\frac{0.09}{12}\right)^{12*5}-1\right)}{\left(\frac{0.09}{12}\right)}\)
    Or, =FV(0.09/12,12*5,130)
    In 25 more years: \(9805.14(1+\frac{0.09}{12})^{12*25}\)
    =FV(0.09/12,12*25,0,9805.14)
    Your final balance will be $92,250.82.
  2. \(92250.82 - 130*5*12\text{.}\) You will earn $84,450.82 in interest.
  3. \(84450.82/92250.82\text{.}\) The final balance will be about 91.5% interest.

3.3.6.7.

Solution.
\(\frac{3500\left(\frac{0.038}{12}\right)}{\left(1+\frac{0.038}{12}\right)^{30}-1}\)
=PMT(0.038/12,30,0,3500)
You should deposit $111.40 each month.

3.3.6.9.

Solution.
\(\frac{450000\left(\frac{0.06}{12}\right)}{\left(1+\frac{0.06}{12}\right)^{12*30}-1}\)
Or, =PMT(0.06/12,12*30,0,450000)
Jamie needs to deposit $447.98 each month.

3.3.6.11.

Solution.
  1. Jose: \(55000\left(1+\frac{0.056}{12}\right)^{12*25}\)
    Or, =FV(0.056/12,12*25,0,55000)
    Jose’s partner:\(\frac{375\left(\left(1+\frac{0.056}{12}\right)^{12*25}-1\right)}{\left(\frac{0.056}{12}\right)}\)
    Or, =FV(0.056/12,12*25,375)
    Jose will have $222,310.85 and his partner will have $244,447.68.
  2. Jose: \(222310.85 - 55000\)
    Jose’s partner: \(244447.68 - 375*12*25\)
    Jose will earn $167,310.85 and his partner will earn $131,947.68 in interest.
  3. Jose: \(167310.85/222310.85\)
    Jose’s partner: \(131947.68/244447.68\)
    Jose’s final balance will be about 75.3% interest and Jose’s partner’s final balance will be about 54.0% interest.

3.3.6.13.

Solution.
  1. \(1000\left(1+\frac{0.045}{12}\right)^{12*10}+\frac{100\left(\left(1+\frac{0.045}{12}\right)^{12*10}-1\right)}{\frac{0.045}{12}}\)
    Or, =FV(0.045/12,12*10,100,1000)
    Sylvin will have a final balance of $16,686.80.
  2. \(16686.8 - (1000 + 100*12*10)\text{.}\) Sylvin will earn $3,686.80 in interest.
  3. \(3686.8/16686.8\text{.}\) The final balance will be about 22.1% interest.

3.3.6.15.

Solution.
  1. \(\frac{100\left(\left(1+\frac{0.04}{12}\right)^{12*25}-1\right)}{\frac{0.04}{12}}\)
    Or, =FV(0.04/12,12*25,100)
    Vanessa will have $51,412.95 when she turns 65.
  2. \(\frac{100\left(\left(1+\frac{0.04}{12}\right)^{12*40}-1\right)}{\frac{0.04}{12}}\)
    =FV(0.04/12,12*40,100)
    Vanessa would have $118,196.13 if she had started saving when she was 25.

3.3.6.17.

Solution.
  1. \(\frac{50\left(\left(1+\frac{0.035}{52}\right)^{52*18}-1\right)}{\frac{0.035}{52}}\)
    Or, =FV(0.035/52,52*18,50)
    They will have saved $65,164.37 after 18 years.
  2. \(\frac{65164.37}{(1+\frac{0.035}{52})^{52*18}}\)
    Or, =PV(0.035/52,52*18,0,65164.37)
    They would have needed an deposit of $34,713.37.

3.4 Loan Payments
3.4.9 Exercises

3.4.9.1.

Solution.
  1. \(P = \frac{700\left(1-\left(1+\frac{5.5\%}{12}\right)^{-12\times 30}\right)}{\frac{5.5\%}{12}}\text{,}\) which gives \(P \approx \$123,285.23\)
    or =PV(5.5%/12,12*30,-700) [Note 700 is entered as negative, to signify a payment]
  2. \(700 * 12 * 30\) dollars, or $252,000.00 in total payments to the loan company
  3. Interest will be the difference between the total payments, and the amount borrowed. So the interest on this loan is \(\$252,000.00 - \$123,285.23 = \$128,714.77\text{.}\)

3.4.9.3.

Solution.
\(d = \frac{25000\left(\frac{2\%}{12}\right)}{\left(1-\left(1+\frac{2\%}{12}\right)^{-12 \times 4}\right)}\text{,}\) which gives \(d \approx \$542.38\)
or =PMT(2%/12,48,25000)

3.4.9.5.

Solution.
  1. The loan amount will be 90% of $200,000.00
    \begin{gather*} = (0.9 * \$200,000.00)\\ = \$180,000.00 \end{gather*}
  2. \(d = \frac{180000\left(\frac{5\%}{12}\right)}{\left(1-\left(1+\frac{5\%}{12}\right)^{-12 \times 30}\right)}\text{,}\) which gives \(d \approx \$966.28\)
    or =PMT(5%/12,12*30,180000)
  3. \(d = \frac{180000\left(\frac{6\%}{12}\right)}{\left(1-\left(1+\frac{6\%}{12}\right)^{-12 \times 30}\right)}\text{,}\) which gives \(d \approx \$1,079.19\)
    or =PMT(6%/12,12*30,180000)

3.4.9.7.

Solution.
First, we need to find out the amount of the monthly payments for this loan.
\(d = \frac{24000\left(\frac{3\%}{12}\right)}{\left(1-\left(1+\frac{3\%}{12}\right)^{-12 \times 5}\right)}\text{,}\) which gives \(d \approx \$431.25\)
or =PMT(3%/12,12*5,24000)
The amount still owed three years later, is the present value of the two years of remaining payments on the loan.
\(P = \frac{\left(1-\left(1+\frac{3\%}{12}\right)^{-12 \times 2}\right)}{\frac{3\%}{12}}\text{,}\) which gives \(P \approx \$10,033.45\)
or =PV(3%/12,12*2,-431.25)

3.4.9.9.

Solution.
=PV(4%/12,12*30,950) which gives $198,988.18.
Now add $20,000 to this balance, which gives $218,988.18.

3.4.9.11.

Solution.
  1. =PMT(5%,10,100000,0) which gives $12,950.46.
  2. The total payments will be $129,504.60.
    The interest is the amount over the $100,000 initial investment, or $29,504.60.
    The percentage of the total payment sum representing interest will be \(100*(29,504.60/129,504.60)\%\text{,}\) or approximately 22.7827%.

3.4.9.13.

Solution.
  1. =PMT(4.5%/12,12*30,250000) which gives $1,266.71.
  2. This will be the present value of the remaining 240 loan payments:
    =PV(4.5%/12,12*20,1266.71) which gives $200,223.07.
  3. This will be the present value of the remaining 120 loan payments:
    =PV(4.5%/12,12*10,1266.71) which gives $122,223.99.
  4. At the beginning of the repayment period, most of each payment goes to interest (thus the loan balance reduces very slowly at first). Over time, more of each payment shifts to principal, and less to interest. At the end of the loan repayment period, nearly all the payment is going to principal.

3.4.9.15.

Solution.
=FV(0.035/12,3*12,200,0) = $7,579.95. Paul will have $7,579.95 in 3 years.

3.4.9.17.

Solution.
=PV(0.028/12,4*12,100,0) = $4,535.96. Miao can finance $4,535.96 in equipment to have a monthly loan payment of $100 for 4 years.

3.4.9.19.

Solution.
=PMT(0.043/12,30*12,364500,0) = $1,803.81. Their mortgage payment would be $1,803.81.

3.4.9.21.

Solution.
For the first plan: =FV(0.048/12,20*12,150,0) = $60,251.26. Zahid would have $60,251.26 if he puts in $150 per month for 20 years.
For the second plan: =FV(0.048/12,10*12,300,0) = $46,089.59. Zahid would only have $46,089.59 if he waited and put in $300 per month for 10 years.

3.5 Income Taxes
3.5.14 Exercises

3.5.14.1.

Solution.
A credit decreases your bill more. It decreases your bill by the full amount of the credit. A deduction only decreases your tax bill by a percentage.

3.5.14.3.

Solution.
The amount of taxes owed is decreased by $60 because 12% of $500 is $60.

3.5.14.5.

Solution.
Yes, you can make adjustments and take a deduction. Adjustments to your income happen before deductions.

3.5.14.7.

Solution.
She should itemize because itemizing reduces her taxable income by $13,000. The standard deduction would have reduced her taxable income by $12,000.

3.5.14.9.

Solution.
No, he should not be concerned. Only the $1000 will be taxed at 22%. The rest of his income will be taxed at a lower level.

3.5.14.11.

Solution.
There is a total of $31,500 between $10,275 and $41,775. 12% of $29,175 is $3,780.

3.5.14.13.

Solution.
$16,589 in taxes minus $13,456 for withholdings, and they can claim and $2,500 in credits. This leaves them owing $633.

3.5.14.15.

Solution.
  1. Take the income minus the adjustments \(125000-5600=\$119,400\text{.}\) Their adjusted gross income is $119,400.
  2. They should take the standard deduction because itemizing saves them less.
  3. Taxable income: \(119400-25900=93500\)
    Taxes owed: \(9615+0.22*(93500-83500)=\$11,815\)
    They owe $11,815 in taxes.
  4. \(11815-15000=-\$3,185\) Take the taxes owed minus credits and withholdings. They will receive a refund for $3,185.

3.5.14.17.

Solution.
  1. Gross Income: \(76000+750 = \$76,750\)
  2. Adjusted Gross Income: \(76750-25000 = \$51,750\)
  3. She should take itemized deductions since they are greater than the standard deduction for head of household.
  4. Taxable Income: \(51750-20600 = \$31,150 \)
  5. Tax from Table: \(1465+0.12*(31150-14650) = \$3,445\text{.}\) Owed/Refund: \(3445 – 4200 – 6300 = - \$7,055\)
    Janice will receive a refund for $7,055.

4 Data
4.1 Overview of the Statistical Process
4.1.22 Exercises

4.1.22.1.

Solution.
A sample is a sub group of the population. A population is the entire group of subjects.

4.1.22.3.

Solution.
The intended population is all Grace students.
  1. All PCC Students
  2. 200 students from the Alpha and Beta dorms.
  3. The collected data is not representative of all Grace students since it only includes responses from students living in two dorms. This is an example of sampling bias.

4.1.22.5.

Solution.
  1. The representatives in a state’s congress.
  2. The population size is \(n=106\)
  3. The sample size is in \(n=28\)
  4. The statistic is \(\frac{14}{28}=0.5\) or 50%
  5. The confidence interval is \((45\%, 55\%)\) and tells us that the true percentage of the state congress representatives in support of the new education (the parameter) likely lies between 45% and 55%.

4.1.22.7.

Solution.
The population is all trout in the lake. The sample is the 20 that were caught.

4.1.22.9.

Solution.
Parameter

4.1.22.11.

Solution.
Statistic

4.1.22.13.

Solution.
  1. Stratified
  2. Volunteer
  3. Simple Random Sample

4.1.22.15.

Solution.
  1. Loaded Question
  2. Volunteer Bias
  3. Response Bias
  4. Volunteer
  5. Response Bias
  6. Response Bias or Non-response Bias

4.1.22.17.

Solution.
  1. Observational study
  2. Experiment
  3. Observational study

4.1.22.19.

Solution.
  1. Cancer patients
  2. No because sampling has variability
  3. Stratified
  4. Convenient Sample. It does not represent the population.

4.1.22.21.

Solution.
  1. All students
  2. Experiment
  3. It is only looking at one class and not all groups that are in the population so Subjects are not randomly sampled from a specified population.

4.1.22.23.

Solution.
  1. 0.05 or 5%
  2. (25%, 35%)
  3. I am confident that the percentage of college freshmen who prefer morning classes is between 25% to 35%.

4.1.22.25.

Solution.
  1. \((24+36)/2=30\text{.}\) The statistic is 30%.
  2. \(30-24=6\text{.}\) The margin of error is 6%.

4.1.22.27.

Solution.
Play Barry Manilow to half the crop and don’t play any music to the other half of the crop.

4.1.22.29.

Solution.
Answers will vary depending on the article.

4.2 Describing Data
4.2.24 Exercises

4.2.24.1.

Solution.
True

4.2.24.3.

Solution.
  1. Quantitative
  2. Categorical
  3. Categorical
  4. Quantitative
  5. Quantitative

4.2.24.5.

Solution.
Bar graphs and pie charts are used for categorical data.

4.2.24.7.

Solution.
  1. 2 had 3 children.
  2. 15 adults were questioned.
  3. 33.33% of the adults questioned had 0 children.

4.2.24.9.

Solution.
5 students earned and A on their paper.

4.2.24.11.

Solution.
Cory spent $676 on rent this month.

4.2.24.13.

Solution.
  1. This data is categorical.
  2. There are four spaced apart bars labeled Pollution of drinking water, Contamination of soil and water by toxic waste, Air pollution, and Global warming. The x-axis is labeled Environmental Issue and the y-axis is labeled frequncy. Pollution of drinking water goes up to 597, Contamination of soil and drinking water goes up to 526, Air pollution goes up to 455, and Global warming goes up to 354.
  3. No, we cannot make a pie chart out of this data. The total of the relative frequencies is 1932, but only 1012 adults were asked. So some adults selected multiple options.

4.2.24.15.

Solution.
  1. 40 households heat their home with firewood.
  2. 50% of the households heat their home with natural gas.

4.2.24.17.

Solution.
  1. This data is qualitative
  2. Number of cars
    in household    		 Frequency
    0-1 7
    2-3 14
    4-5 3
  3. The histogram is titled "Histogram of number of cars in household". The x-axis is labeled Number of Cars, the scale goes from 0 to 6 and jumps by 1 unit. There are three bars, one from 0-2, one from 2-4, and one from 4-6. The y-axis is labeled Frequency and the scale goes from 0 to 16 by units of two. The 0-2 bar goes to 7, the 2-4 bar goes to 14, and the 4-6 bar goes to 3.
  4. This data is unimodal and skewed right, with no outliers.

4.2.24.19.

Solution.
The graph would be more effective at displaying the true differences between the categories if the vertical scale started at 0. The vertical axis is missing a label and units, so we can’t tell if those are frequencies or relative frequencies. A flat bar graph (instead of the 3d graph) would be easier to read.

4.2.24.21.

Solution.
This is a poor graph because the vertical axis does not have a numerical scale, so we cannot know how many have each drink as a favorite drink. We also don’t know if the bottom vertical line represents 0, which is potentially misleading.

4.2.24.23.

Solution.
  1. Normal distribution – The number of heads in 24 sets of 100 coin flips.
  2. Positive or right skewed – Distribution of scores on a psychology test.
  3. Negative or left skewed – Scores on a 20-point statistics quiz.
  4. Bimodal – The frequency of times between eruptions of the Old Faithful geyser.

4.2.24.25.

Solution.
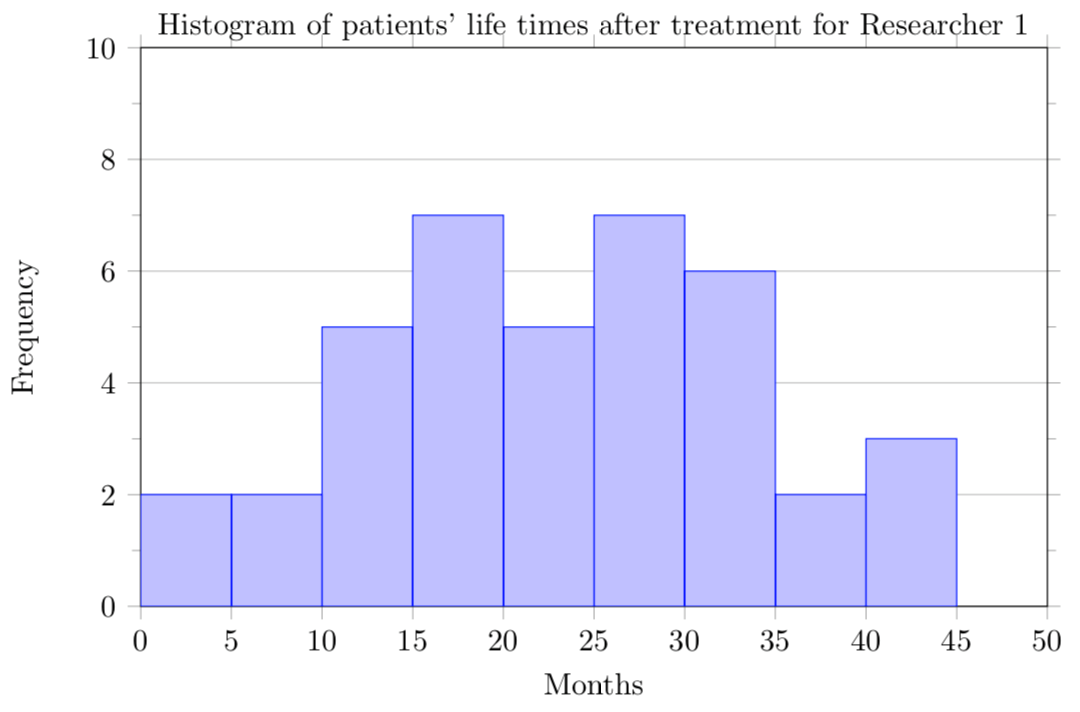
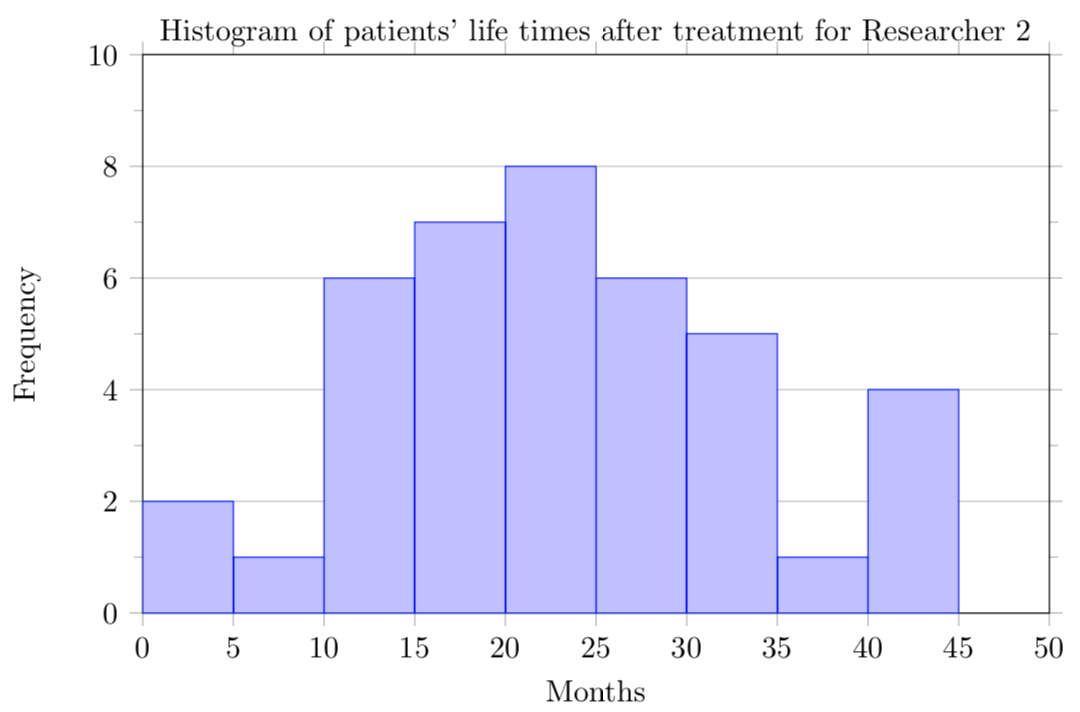
  2. The data for patients of both researchers is symmetric. Researcher’s 1 patients’ data appears to be unimodal, but Researcher 2’s patients’ data may be bimodal or multimodal. The data for Researcher 1’s patients does not have any outliers, but the data for Researcher’s 2 may have outliers between 0 and 5 months or 40 and 45 months.

4.3 Summary Statistics: Measures of Center
4.3.7 Exercises

4.3.7.1.

Solution.
  1. In Excel:
    =average(7.50,25.00,10.00,10.00,7.50,8.25,9.00,5.00,15.00,8.00,7.25,7.50,8.00,7.00,12.00)
    \(=\$9.80\)
    There are 15 times shown, so \(n=15\text{.}\) The mean is:
    \begin{align*} \bar{x} \amp= \frac{(7.50+25.00+10.00+10.00+7.50+8.25+9.00+5.00+15.00+8.00+7.25+7.50+8.00+7.00+12.00)}{15}\\ \amp=\$9.80 \end{align*}
  2. In Excel:
    =median(7.50,25.00,10.00,10.00,7.50,8.25,9.00,5.00,15.00,8.00,7.25,7.50,8.00,7.00,12.00)
    \(=\$8.00\)
    There are 15 times shown, so \(n=15\text{.}\) We start by listing the data in order:
    $5.00, $7.00, $7.25, $7.50, $7.50, $7.50, $8.00, $8.00, $8.25, $9.00, $10.00, $10.00, $12.00, $15.00, $25.00
    \(Median=\$8.00\)
  3. Since the mean is greater than the median, we would expect the distribution will be skewed right.

4.3.7.3.

Solution.
  1. In Excel:
    =average(15.2,18.8,19.3,19.7,20.2,21.8,22.1,29.4)
    \(=20.81\) seconds
    There are 8 times shown, so \(n=8\text{.}\)
    \begin{align*} \bar{x} \amp= \frac{(15.2+18.8+19.3+19.7+20.2+21.8+22.1+29.4)}{15}\\ \amp=20.81 \text{ seconds} \end{align*}
  2. In Excel:
    =median(15.2,18.8,19.3,19.7,20.2,21.8,22.1,29.4)
    \(=19.95\) seconds
    There are 8 times shown, so \(n=8\text{.}\) The times are given already in order:
    15.2, 18.8, 19.3, 19.7, 20.2, 21.8, 22.1, 29.4
    \begin{align*} Median\amp=\frac{19.7+20.2}{2}\\ \amp=19.95 \text{ seconds} \end{align*}
  3. Since the mean and median are approximately equal, we would expect that the distribution is symmetric.

4.3.7.5.

Solution.
  1. In GeoGebra Classic, enter the costs into the column A and frequencies into column B of the spreadsheet and use the “One Variable Analysis” function. Then use the “Show Statistics” option.
    \begin{gather*} Mean=33.8 \text{ thousand dollars} \end{gather*}
    The sum of the frequencies is 75, so \(n=75\)
    \begin{align*} \bar{x}\amp=\frac{15⋅3+20⋅7+25⋅10+30⋅15+35⋅13+40⋅11+45⋅9+50⋅7}{75}\\ \amp=33.8 \text{ thousand dollars} \end{align*}
  2. In GeoGebra Classic, enter the costs into the column A and frequencies into column B of the spreadsheet and use the “One Variable Analysis” function. Then use the “Show Statistics” option.
    \begin{gather*} Median=35 \text{ thousand dollars} \end{gather*}
    Since there are 75 values (an odd number), we know that the median will be the single middle data value. Because \(\frac{75}{2}=37.5\text{,}\) we know it will be the 38th value in the list. The 38th value is 35, so the median is 35 thousand dollars.
  3. Since the mean is less than the median, we would expect the distribution to be skewed left.

4.3.7.7.

Solution.
  1. For Researcher 1:
    In Excel:
    =average(3,4,11,15,16,17,22,44,37,16,14,24,25,15,26,27,33,29,35,44,13,21,22,10,12,8,40,32,26,27,31,34,29,17,8,24,18,47,33,34)
    \(=23.6\) months.
    =median(3,4,11,15,16,17,22,44,37,16,14,24,25,15,26,27,33,29,35,44,13,21,22,10,12,8,40,32,26,27,31,34,29,17,8,24,18,47,33,34)
    \(=24\) months
    The mean for Researcher 1’s patients is 23.6 months, and the median for Researcher’s 1 patients is 24 months.
    For Researcher 2:
    In Excel:
    =average(3,14,11,5,16,17,28,41,31,18,14,14,26,25,21,22,31,2,35,44,23,21,21,16,12,18,41,22,16,25,33,34,29,13,18,24,23,42,33,29)
    \(=22.8\) months
    =median(3,14,11,5,16,17,28,41,31,18,14,14,26,25,21,22,31,2,35,44,23,21,21,16,12,18,41,22,16,25,33,34,29,13,18,24,23,42,33,29)
    \(=22\) months
    The mean for Researcher 2’s patients is 22.8 months, and the median is 22 months
  2. Both the mean and median for Researcher 1’s patients are greater than the mean and median for Researcher 2’s patients. So, on average, Researcher 1’s patients have a longer life time after starting the cancer treatment than Researcher 2’s patients.

4.3.7.9.

Solution.
GeoGebra was used to create the histograms. You should check with your instructor to see if histograms are to be hand-drawn or computer generated. Answers will vary depending on the size of the margins and the programs you are using.
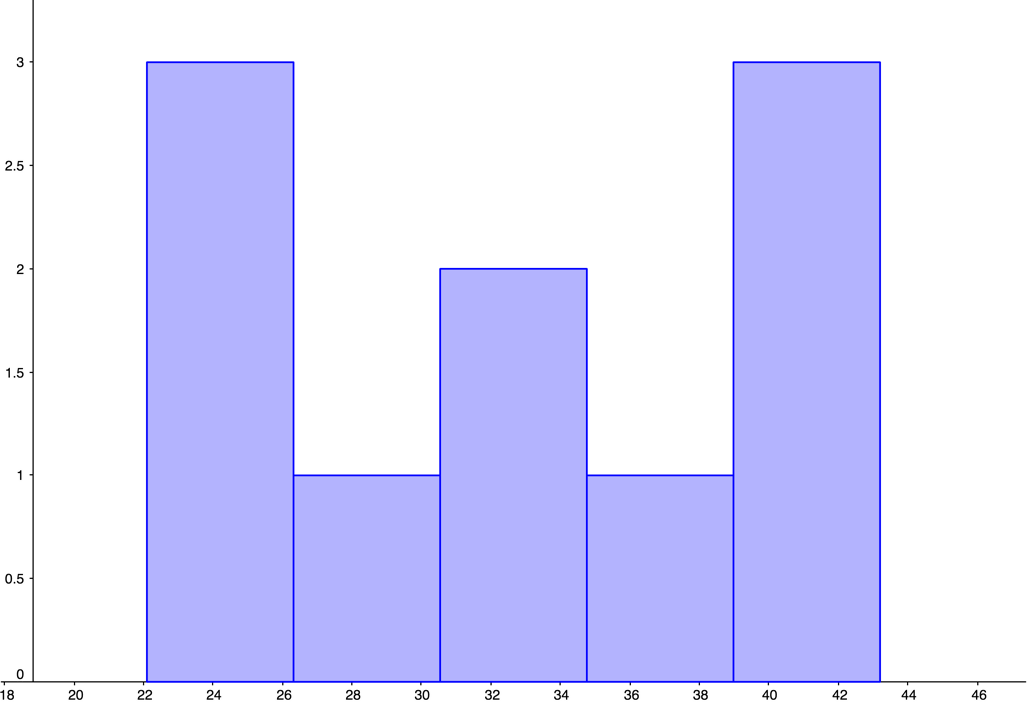
  1. Figure 4.3.15. Histogram for Average Number of Pieces Correctly Remembered by Non-players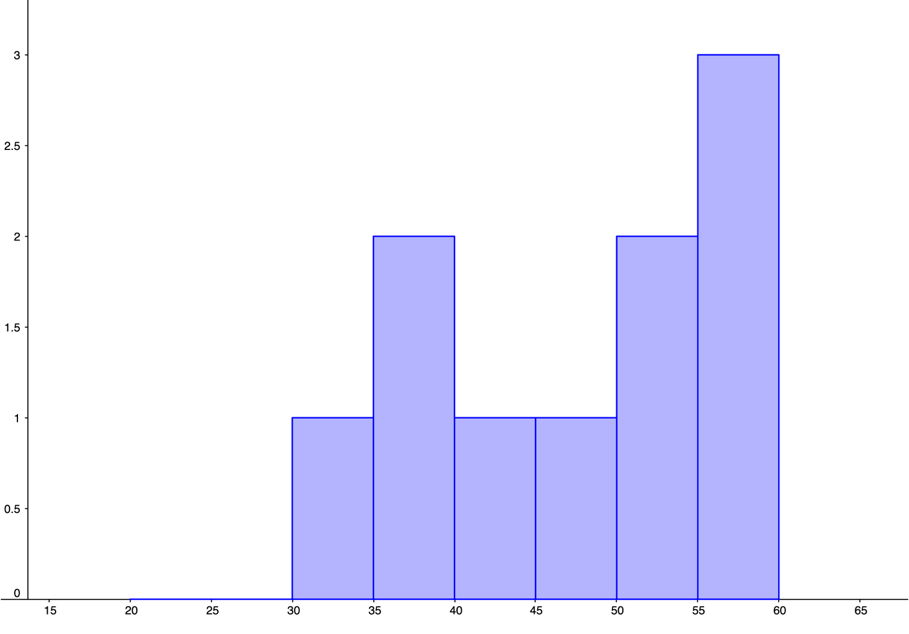
    Figure 4.3.16. Histogram for Average Number of Pieces Correctly Remembered by Beginners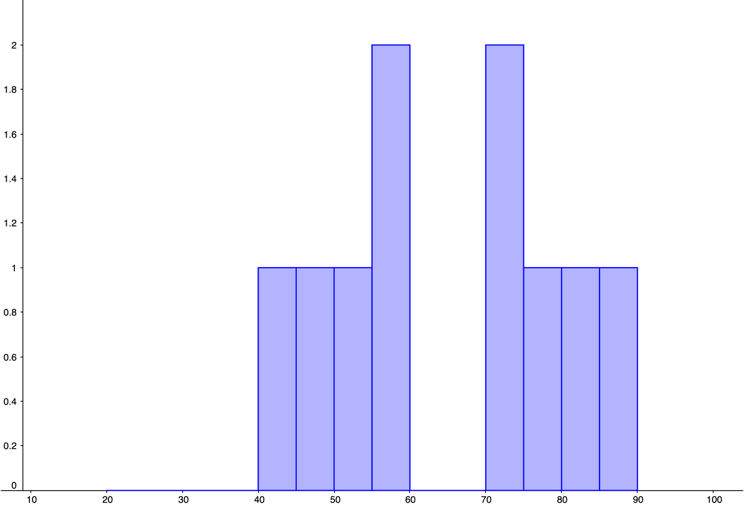
    Figure 4.3.17. Histogram for Average Number of Pieces Correctly Remembered by Tournament Players
  2. The mean number of pieces correctly remembered for non-players was 33.65 pieces.
    The mean number of pieces correctly remembered for beginners was 47.6 pieces.
    The mean number of pieces correctly remembered for tournament players was 64.98 pieces.
  3. The median number of pieces correctly remembered for non-players was 33.5 pieces.
    The median number of pieces correctly remembered for beginners was 51.3 pieces.
    The median number of pieces correctly remembered for tournament players was 71.1 pieces.
  4. The distribution for non-players appears to be uniform. The distribution for beginners looks unimodal and left-skewed. The distribution for tournament players appears bimodal and symmetric.
    The mean and median number of pieces correctly remembered were both greatest for tournament players, with non-players having the smallest mean and median of pieces correctly remembered.

4.3.7.11.

Solution.
  1. There are many possible answers for this problem. Three data sets with 5 values each that have the same mean but different medians are:
    0, 0, 0, 0, 10
    0, 0, 2, 4, 4
    0, 1, 1, 1, 7
  2. There are many possible answers for this problem. Three data sets with 5 values that have the same median but different means are:
    10, 10, 10, 10, 10
    0, 0, 10, 15, 20
    1, 5, 10, 10, 10

4.3.7.13.

Solution.
  1. This graph is skewed left.
  2. I expect that the mean is less than the median because the graph is skewed left.

4.3.7.15.

Solution.
Answers will vary.

4.4 Summary Statistics: Measures of Variation
4.4.10 Exercises

4.4.10.1.

Solution.
  1. In Excel:
    Entering the data values into cells A1 through A15.
    \begin{align*} s\amp=stdev.s(A1:A15)\\ \amp=\$4.82 \end{align*}
    From Exercise 4.3.7.1, the mean is $9.80. There are 15 data values, so \(n=15\text{.}\)
    We will make a table of data values, their deviations from the mean, and the squared deviations:
    Data Value Deviation Deviation Squared
    \(7.5\) \(7.5-9.8=-2.3\) \((-2.3)^2=5.29\)
    \(25\) \(25-9.8=15.2\) \((15.2)^2=231.04\)
    \(10\) \(10-9.8=0.2\) \((0.2)^2=0.04\)
    \(10\) \(10-9.8=0.2\) \((0.2)^2=0.04\)
    \(7.5\) \(7.5-9.8=-2.3\) \((-2.3)^2=5.29\)
    \(8.25\) \(8.25-9.8=-1.55\) \((-1.55)^2=2.4\)
    \(9\) \(9-9.8=-0.8\) \((-0.8)^2=0.64\)
    \(5\) \(5-9.8=-4.8\) \((-4.8)^2=23.04\)
    \(15\) \(15-9.8=5.2\) \((5.2)^2=27.04\)
    \(8\) \(8-9.8=-1.8\) \((-1.8)^2=3.24\)
    \(7.25\) \(7.25-9.8=-2.55\) \((-2.55)^2=6.5\)
    \(7.5\) \(7.5-9.8=-2.3\) \((-2.3)^2=5.29\)
    \(8\) \(8-9.8=-1.8\) \((-1.8)^2=3.24\)
    \(7\) \(7-9.8=-2.8\) \((-2.8)^2=7.84\)
    \(12\) \(12-9.8=2.2\) \((2.2)^2=4.84\)
    Next, we add the squared deviations and get \(5.29 + 231.04 + 0.04 + 0.04 + 5.29 + 2.4 + 0.64 + 23.04 + 27.04 + 3.24 + 6.5 + 5.29 + 3.24 + 7.84 + 4.84 = 325.78\) dollars-squared.
    The sample standard deviation is:
    \begin{align*} s\amp=\sqrt{\frac{325.78}{14}}\\ \amp=\$4.82 \end{align*}
  2. In GeoGebra:
    In GeoGebra Classic, enter the data values into the column A of the spreadsheet and use the “One Variable Analysis” function. Then use the “Show Statistics” option to find the five-number summary.
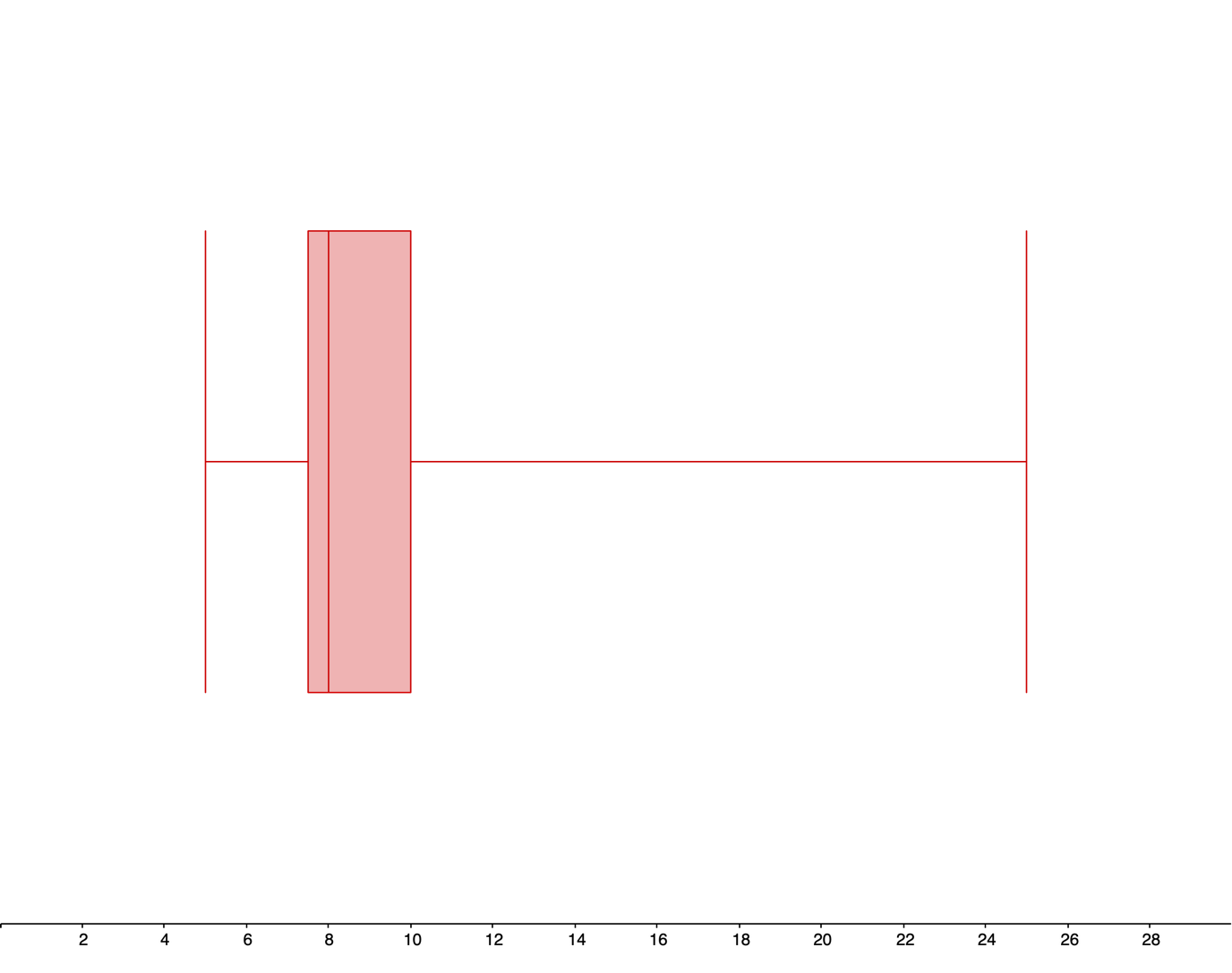
    Min Q1 Median Q3 Max
    $5 $7.50 $8 $10 $25
    From Exercise 4.3.7.1, the data listed in order is:
    $5.00, $7.00, $7.25, $7.50, $7.50, $7.50, $8.00, $8.00, $8.25, $9.00, $10.00, $10.00, $12.00, $15.00, $25.00
    Also from Exercise 4.3.7.1, there are 15 data values (\(n=15\)), and the median is $8.00. The lower half of the data is:
    $5.00, $7.00, $7.25, $7.50, $7.50, $7.50, $8.00
    The median of the lower half is $7.50, so the lower quartile \(Q_{1}\) is $7.50.
    The upper half of the data is:
    $8.25, $9.00, $10.00, $10.00, $12.00, $15.00, $25.00
    The median of the upper half is $10.00, so the upper quartile \(Q_{3}\) is $10.00.
    The smallest and largest data values are $5.00 and 25.00, respectively, so the min and max are $5.00 and $25.00. The five-number summary is:
    Min Q1 Median Q3 Max
    $5 $7.50 $8 $10 $25
  3. The range is:
    \begin{align*} Range \amp= Max - Min\\ \amp=25-5\\ \amp=\$20 \end{align*}
    The interquartile range (IQR) is:
    \begin{align*} IQR \amp= Q_{3} - Q_{1}\\ \amp=10-7.5\\ \amp=\$2.50 \end{align*}

4.4.10.3.

Solution.
  1. In Excel:
    I entered the data values into cells A1 through A9.
    The standard deviation is:
    \begin{align*} s\amp=stdev.s(A1:A9)\\ \amp=4.068 \text{ seconds} \end{align*}
  2. In GeoGebra:
    In GeoGebra Classic, enter the data values into the column A of the spreadsheet and use the “One Variable Analysis” function. Then use the “Show Statistics” option to find the five-number summary.
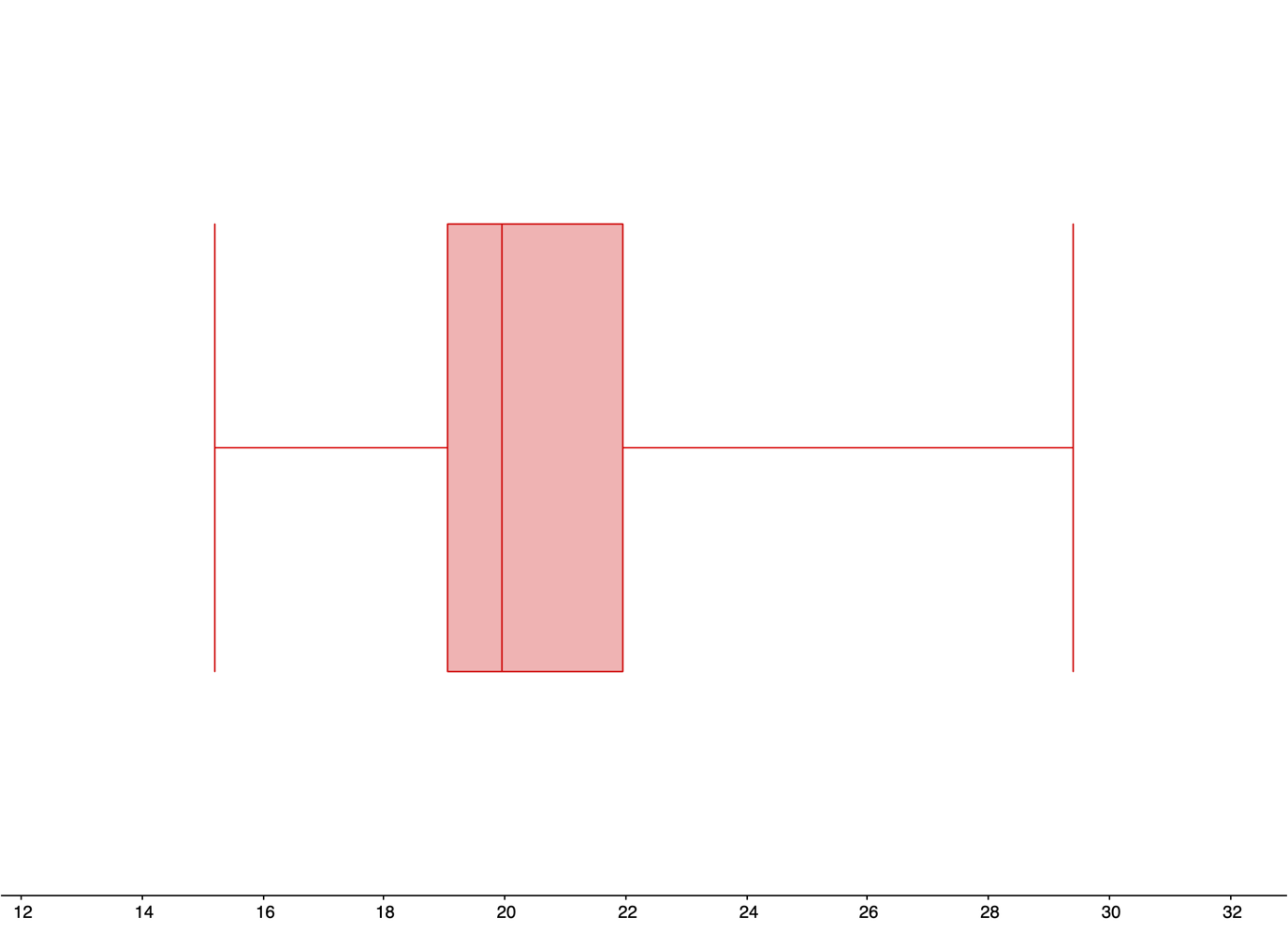
    Min Q1 Median Q3 Max
    15.2 seconds 19.05 seconds 19.95 seconds 21.95 seconds 29.4 seconds
  3. The range is:
    \begin{align*} Range \amp= Max - Min\\ \amp=29.4-15.2\\ \amp=14.2 \text{ seconds} \end{align*}
    The interquartile range (IQR) is:
    \begin{align*} IQR \amp= Q_{3} - Q_{1}\\ \amp=21.95-19.05\\ \amp=2.9 \text{ seconds} \end{align*}

4.4.10.5.

Solution.
  1. In GeoGebra:
    In GeoGebra Classic, enter the costs into column A and frequencies into column B of the spreadsheet and use the “One Variable Analysis” function. Then use the “Show Statistics” option. The standard deviation is:
    \begin{gather*} s=9.58 \text{ thousand dollars} \end{gather*}
    From Exercise 4.3.7.5, the mean is 33.8 thousand dollars.
    The mean and the standaed deviation together tell us that, on average, the cars at the local dealership are $9,580 from the mean price of $33,800.
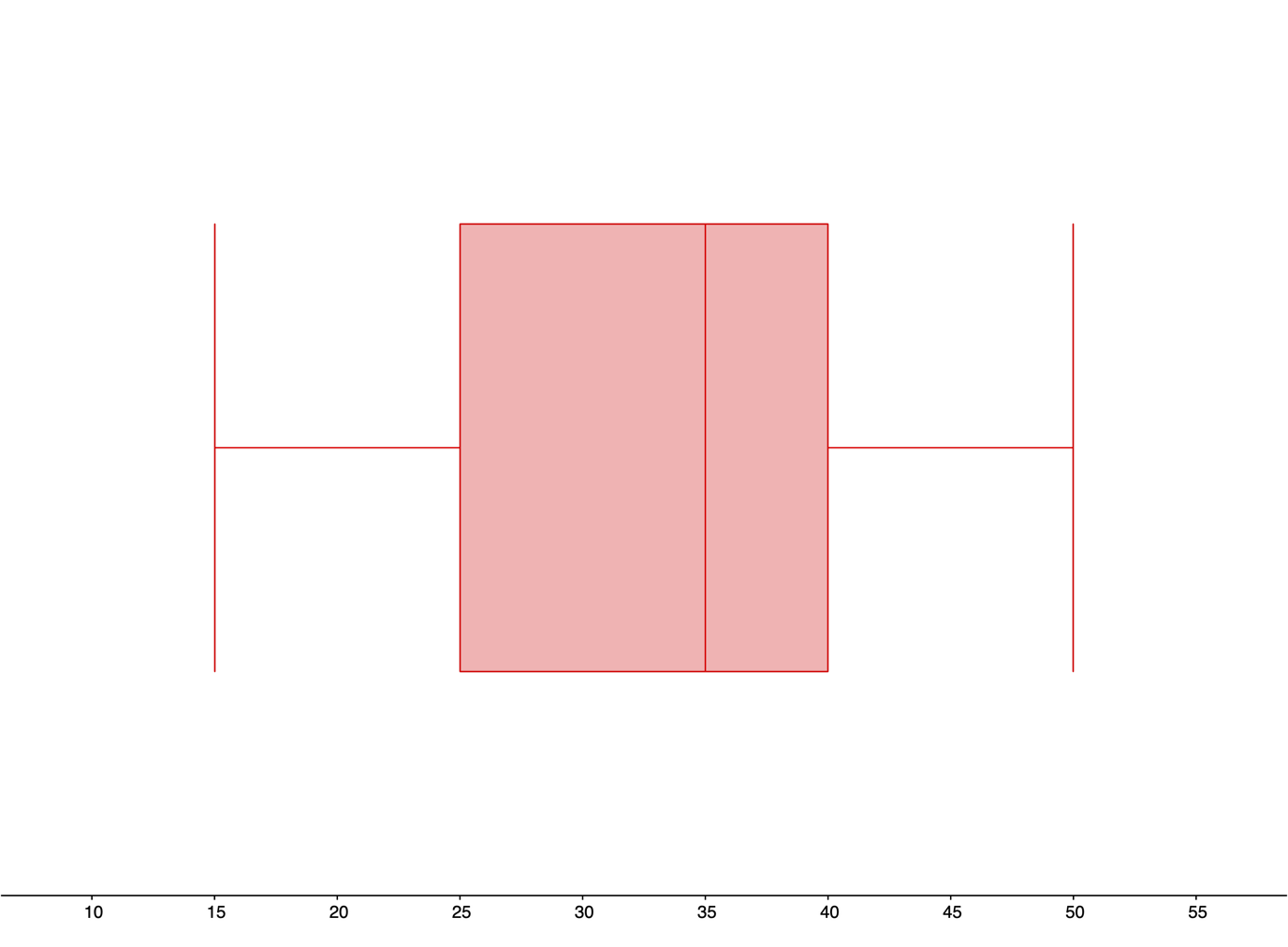
  2. In GeoGebra:
    In GeoGebra Classic, enter the data values into the column A of the spreadsheet and use the “One Variable Analysis” function. Then use the “Show Statistics” option to find the five-number summary.
    Min Q1 Median Q3 Max
    15 thousand
    dollars    		 25 thousand
    dollars    		 35 thousand
    dollars    		 40 thousand
    dollars    		 50 thousand
    dollars
  3. The range is:
    \begin{align*} Range \amp= Max - Min\\ \amp=50-15\\ \amp=35 \text{ thousand dollars} \end{align*}
    The interquartile range (IQR) is:
    \begin{align*} IQR \amp= Q_{3} - Q_{1}\\ \amp=40-15\\ \amp=25 \text{ thousand dollars} \end{align*}

4.4.10.7.

Solution.
  1. In GeoGebra:
    In GeoGebra Classic, enter the data values for Researcher 1 into column A of the spreadsheet, and enter the data values for Researcher 2 into column B of the spreadsheet. Then use the “Multiple Variable Analysis” function. Then use the “Show Statistics” function to display the sample standard deviation for each set of data values.
    The sample standard deviation for Researcher 1 is 11.25 months. The sample standard deviation for Research 2 is 11.38 months.
  2. In GeoGebra:
    In GeoGebra Classic, enter the data values for Researcher 1 into column A of the spreadsheet, and enter the data values for Researcher 2 into column B of the spreadsheet. Then use the “Multiple Variable Analysis” function. Then use the “Show Statistics” function to display the sample standard deviation for each set of data values.
    The 5-number summary for Researcher 1 is:
    Min Q1 Median Q3 Max
    3 months 15 months 24 months 32.5 months 47 months
    The 5-number summary for Researcher 2 is:
    Min Q1 Median Q3 Max
    2 months 16 months 22 months 30 months 44 months
  3. The range for Researcher 1 is:
    \begin{align*} Range \amp= Max - Min\\ \amp=47-3\\ \amp=44 \text{ months} \end{align*}
    The interquartile range (IQR) for researcher 1 is:
    \begin{align*} IQR \amp= Q_{3} - Q_{1}\\ \amp=32.5-15\\ \amp=17.5 \text{ months} \end{align*}
    The range for Researcher 2 is:
    \begin{align*} Range \amp= Max - Min\\ \amp=44-2\\ \amp=42 \text{ months} \end{align*}
    The interquartile range (IQR) for Researcher 2 is:
    \begin{align*} IQR \amp= Q_{3} - Q_{1}\\ \amp=30-16\\ \amp=14 \text{ months} \end{align*}
  4. In GeoGebra Classic, enter the data values for Researcher 1 into column A of the spreadsheet, and enter the data values for Research 2 into column B of the spreadsheet. Then use the “Multiple Variable Analysis” function. Then select “Stacked BoxPlots” from the drop-down menu.
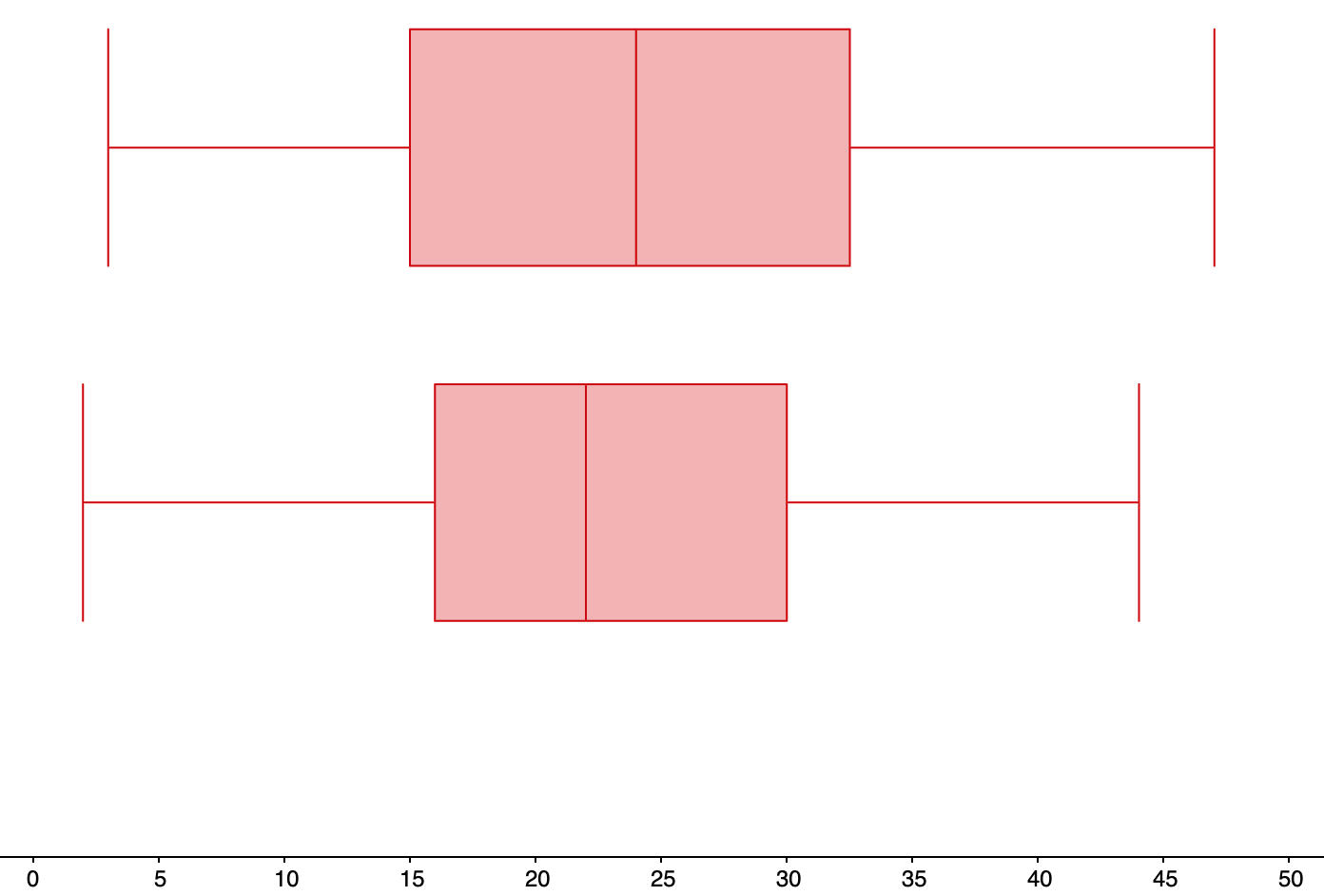    Researcher 1 has a larger minimum, median, 3rd quartile, and maximum than Researcher 2. For Researcher 1, 50% of the patients live longer than 24 months after treatment, compared to 50% of patients living longer than 22 months after treatment for Researcher 1.
    Researcher 2 has less variation in the life times than Researcher 1, with an IQR of 14 months for Researcher 2, compared to an IQR 16.5 months for Researcher 1.

4.4.10.9.

Solution.
  1. In GeoGebra:
    In GeoGebra Classic, enter the data values for non-players into column A of the spreadsheet, enter the data values for beginners into column B of the spreadsheet, and enter the data value for tournament players into column C of the spreadsheet. Then use the “Multiple Variable Analysis” function. Then use the “Show Statistics” function to display the sample standard deviation for each set of data values.
    The sample standard deviation for non-players is 8.033 chess pieces. The sample standard deviation for beginners is 9.031 chess pieces. The sample standard deviation for tournament players is 15.622 chess pieces.
  2. In GeoGebra:
    In GeoGebra Classic, enter the data values for non-players into column A of the spreadsheet, enter the data values for beginners into column B of the spreadsheet, and enter the data value for tournament players into column C of the spreadsheet. Then use the “Multiple Variable Analysis” function. Then use the “Show Statistics” function to display the sample standard deviation for each set of data values.
    The 5-number summary for non-players is:
    Min Q1 Median Q3 Max
    22.1 chess
    pieces    		 26.2 chess
    pieces    		 32.6 chess
    pieces    		 39.7 chess
    pieces    		 43.2 chess
    pieces
    The 5-number summary for beginners is:
    Min Q1 Median Q3 Max
    32.5 chess
    pieces    		 39.1 chess
    pieces    		 48.4 chess
    pieces    		 55.7 chess
    pieces    		 57.7 chess
    pieces
    The 5-number summary for tournament palyers is:
    Min Q1 Median Q3 Max
    40.1 chess
    pieces    		 51.2 chess
    pieces    		 64.6 chess
    pieces    		 75.9 chess
    pieces    		 85.3 chess
    pieces
  3. The range for non-players is:
    \begin{align*} Range \amp= Max - Min\\ \amp=43.2-22.1\\ \amp=21.2 \text{ chess pieces} \end{align*}
    The interquartile range (IQR) for non-players is:
    \begin{align*} IQR \amp= Q_{3} - Q_{1}\\ \amp=39.7-26.2\\ \amp=13.5 \text{ chess pieces} \end{align*}
    The range for beginners is:
    \begin{align*} Range \amp= Max - Min\\ \amp=57.7-32.5\\ \amp=25.2 \text{ chess pieces} \end{align*}
    The interquartile range (IQR) for beginners is:
    \begin{align*} IQR \amp= Q_{3} - Q_{1}\\ \amp=55.7-39.1\\ \amp=16.6 \text{ chess pieces} \end{align*}
    The range tournament players for is:
    \begin{align*} Range \amp= Max - Min\\ \amp=85.3-40.1\\ \amp=45.2 \text{ chess pieces} \end{align*}
    The interquartile range (IQR) for tournament players is:
    \begin{align*} IQR \amp= Q_{3} - Q_{1}\\ \amp=75.9-51.2\\ \amp=24.7 \text{ chess pieces} \end{align*}
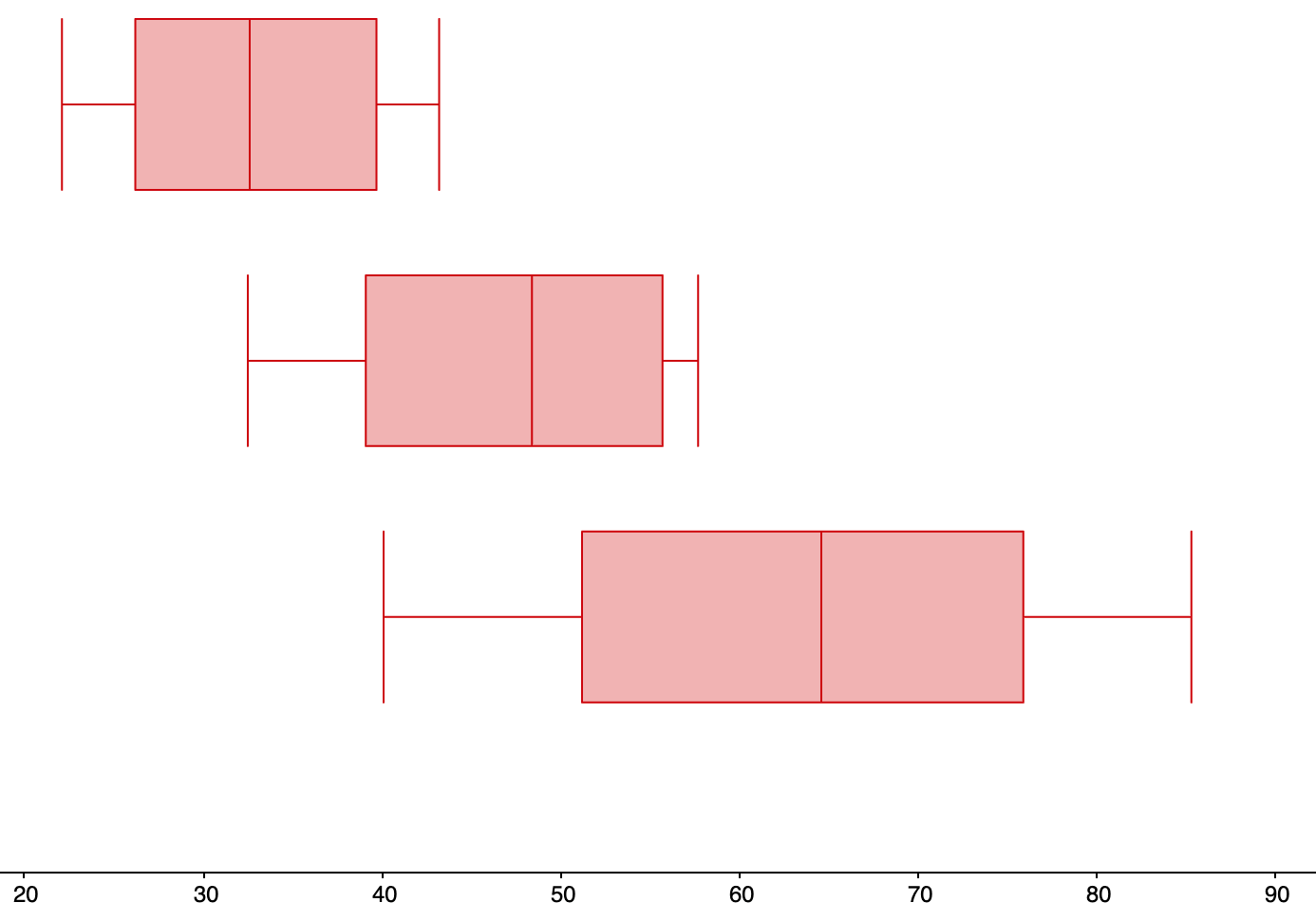  4. Tournament players did the best at remembering positions (as shown by all of the numbers of their 5-number summary being larger than the corresponding numbers for the other two groups). However, tournaments players were not completely superior to the other two groups; the best non-players remembered more chess pieces than the worst tournament players. Also tournament players had more variation in how much they.

4.4.10.11.

Solution.
  1. There are many possible answers for this question. The data sets \({10, 10, 10, 10, 10}\) and \({9, 9, 10, 11, 11}\) have the same mean (10) but different standard deviations (0 and 1, respectively).
  2. There are many possible answers for this question. The data sets \({2, 2, 2, 2, 2}\) and \({9, 9, 9, 9, 9}\) have the same standard deviation (0) but different means (2 and 9, respectively).

4.4.10.13.

Solution.
  1. The 25th, 50th, and 75th percentiles are, respectively, the 1st quartile, median, and 3rd quartile for the data sets. Reading the boxplot for CPAs, the 25th, 50th, and 75th percentiles for CPAs’ salaries are, respectively, $40,000, $75,000, and $90,000. Reading the boxplot for actuaries, the 25th, 50th, and 75th percentiles for actuaries’ salaries are, respectively, $75,000, $90,000, and $94,000
  2. Deshawn’s salary (the median salary for an actuary) is $90,000; Kelsey’s salary (the first quartile salary) is also $75,000. So Deshawn makes more than Kelsey, by $15,000.
  3. 75% of actuaries make more than the median salary of a CPA ($75,000).
  4. 25% of all CPAs earn less than all actuaries.

4.4.10.15.

Solution.
  1. \begin{align*} Z\amp=\frac{\text{data value}-\text{mean}}{\text{standard deviation}}\\ \amp=\frac{21.4-25}{1.15}\\ \amp=-3.13 \text{ standard deviations} \end{align*}
  2. The \(Z\)-score for the gas mileage of the car is -3.13 standard deviations.

4.4.10.17.

Solution.
  1. In GeoGebra:
    In GeoGebra Classic, enter the data values into the column A of the spreadsheet and use the “One Variable Analysis” function. Then use the “Show Statistics” option to find the mean and standard deviation.
    The mean is 46.2 hours per year, and the standard deviation is 6.16 hours per year.
  2. \begin{align*} Z\amp=\frac{\text{data value}-\text{mean}}{\text{standard deviation}}\\ \amp=\frac{42-46.2}{6.16}\\ \amp=-0.68 \text{ standard deviations} \end{align*}
    The \(Z\)-score for a city with an average delay time of 42 hours per year is -0.68 standard deviations.

4.4.10.19.

Solution.
\begin{align*} Z_{Math}\amp=\frac{\text{data value}-\text{mean}}{\text{standard deviation}}\\ \amp=\frac{89-75}{7}\\ \amp=2 \text{ standard deviations} \end{align*}
\begin{align*} Z_{English}\amp=\frac{\text{data value}-\text{mean}}{\text{standard deviation}}\\ \amp=\frac{65-53}{4}\\ \amp=3 \text{ standard deviations} \end{align*}
Because the \(Z\)-score of my English test is greater than the \(Z\)-score of my math test, I did better on the English test than I did on the math test.

4.4.10.21.

Solution.
\begin{align*} Z_{Poe}\amp=\frac{\text{data value}-\text{mean}}{\text{standard deviation}}\\ \amp=\frac{20.2-16.5}{1.85}\\ \amp=2 \text{ standard deviations} \end{align*}
\begin{align*} Z_{Gibson}\amp=\frac{\text{data value}-\text{mean}}{\text{standard deviation}}\\ \amp=\frac{107-81}{13}\\ \amp=2 \text{ standard deviations} \end{align*}
Because the \(Z\)-scores for the heights of Poe (the Clydesdale horse) and Gibson (the Great Dane) are the same, neither animal is taller than the other when compared to their respective breeds.

5 Math Models
5.5 Carbon Dioxide Lab

5.5.1.
5.5.1.a
Solution.
See note on part d.
\(a \approx 1.5\text{,}\) \(b \approx 297\)
5.5.1.b
Solution.
See note on part d.
\(c \approx 29.7\text{,}\) \(d \approx 0.0216\)
5.5.1.c
Solution.
See note on part d.
\(f \approx 86\text{,}\) \(g \approx 260\)
5.5.1.d
Solution.
I usually grade this problem by their graph, and I tend to grade by effort. If you’re unsure, approximate answers are given above. 15 points for all four parts.
5.5.3.
5.5.3.a
Solution.
The \(\text{CO}_2\) increases by about 1.5 (or their \(a\)) ppm every year. (3 points)
5.5.3.b
Solution.
The \(\text{CO}_2\) ppm increases exponentially by about 2.2% (or their \(d \times 100\%\)) every year. (4 points)
5.5.3.c
Solution.
The \(\text{CO}_2\) levels repeat periodically every 260 years. (3 points)
5.5.5.
5.5.5.a
Solution.
Give 4 points for a plot that roughly matches the plot above.
5.5.5.b
Solution.
4 points for answering “exponential model,” and if they answer incorrectly, then give partial credit up to 2 points if they justify their answer, but no points for unjustified incorrect answers.
5.5.5.c
Solution.
3 points for pointing out something wrong with the model they chose in part b, 4 points for pointing out something useful. Take off up to 2 points each for bad or insufficient reasoning.
5.5.7.
5.5.7.a
Solution.
Answers will vary. I’m looking for the students to show that they understand that choosing which data to consider can affect the average of the data. 5 points.
5.5.7.b
Solution.
Answers will vary. Grade on how much their answer makes sense, but be lenient or at least make helpful commments if you take off points because we do not want students to believe they are losing points for their opinions or political beliefs.

6 Democracy
6.1 Apportionment
6.1.10 Exercises

6.1.10.1.

Solution.
  1. Math: 6 tutors, English: 5 tutors, Chemistry: 3 tutors, Biology: 1 tutor
  2. Math: 7 tutors, English: 5 tutors, Chemistry: 2 tutors, Biology: 1 tutor, Modified divisor 47
  3. Math: 6 tutors, English: 5 tutors, Chemistry: 3 tutors, Biology: 1 tutor, Modified divisor 52
  4. Math: 6 tutors, English: 5 tutors, Chemistry: 3 tutors, Biology: 1 tutor, Divisor 53

6.1.10.3.

Solution.
  1. Morning: 1 salesperson, Midday: 5 salespeople, Afternoon: 6 salespeople, Evening: 8 salespeople
  2. Morning: 1 salesperson, Midday: 4 salespeople, Afternoon: 7 salespeople, Evening: 8 salespeople, Modified divisor 62
  3. Morning: 1 salesperson, Midday: 5 salespeople, Afternoon: 6 salespeople, Evening: 8 salespeople, Divisor 67.5
  4. Morning: 1 salesperson, Midday: 5 salespeople, Afternoon: 6 salespeople, Evening: 8 salespeople, Divisor 67.5

6.1.10.5.

Solution.
  1. Aisha: 18 coins, Basir: 14 coins, Carlos: 4 coins
  2. Aisha: 19 coins, Basir: 14 coins, Carlos: 3 coins, Modified divisor 400
  3. Aisha: 19 coins, Basir: 14 coins, Carlos: 3 coins, Modified divisor 410
  4. Aisha: 19 coins, Basir: 14 coins, Carlos: 3 coins, Modified divisor 410

6.1.10.7.

Solution.
  1. A: 5 seats, B: 79 seats, C: 20 seats, D: 12 seats
  2. A: 4 seats, B: 80 seats, C: 20 seats, D: 12 seats, Modified divisor 6950
  3. A: 5 seats, B: 78 seats, C: 20 seats, D: 13 seats, Modified divisor 7128
  4. A: 5 seats, B: 78 seats, C: 20 seats, D: 13 seats, Modified divisor 6950

6.1.10.9.

Solution.
  1. A: 40 seats, B: 24 seats, C: 15 seats, D: 30 seats, E: 10 seats
  2. A: 41 seats, B: 24 seats, C: 14 seats, D: 30 seats, E: 10 seats, Modified divisor 19,700
  3. A: 40 seats, B: 24 seats, C: 15 seats, D: 30 seats, E: 10 seats, Modified divisor 20,100
  4. A: 40 seats, B: 24 seats, C: 15 seats, D: 30 seats, E: 10 seats, Modified divisor 20,125

6.1.10.11.

Solution.
  1. A: 23 seats, B: 16 seats, C: 77 seats, D: 30 seats, E: 21 seats, F: 33 seats
  2. A: 22 seats, B: 16 seats, C: 78 seats, D: 30 seats, E: 21 seats, F: 33 seats, Modified divisor 148.5
  3. A: 23 seats, B: 16 seats, C: 77 seats, D: 30 seats, E: 21 seats, F: 33 seats, Divisor 150
  4. A: 23 seats, B: 16 seats, C: 77 seats, D: 30 seats, E: 21 seats, F: 33 seats, Divisor 150

6.1.10.13.

Solution.
  1. . A: 19 seats, B: 19 seats, C: 22 seats, D: 22 seats, E: 81 seats, F: 87 seats
  2. A: 28 seats, B: 19 seats, C: 22 seats, D: 22 seats, E: 82 seats, F: 87 seats, Modified divisor 4347
  3. A: 19 seats, B: 19 seats, C: 22 seats, D: 22 seats, E: 81 seats, F: 87 seats, Divisor 4400.4
  4. A: 19 seats, B: 19 seats, C: 22 seats, D: 22 seats, E: 81 seats, F: 87 seats, Divisor 4400.4

6.1.10.15.

Solution.
  1. A: 4 seats, B: 4 seats, C: 2 seats
  2. It is not possible to assign 11 seats with Hamilton’s method in this case.
  3. States A and C are the same size, so they have the same decimal value. They would both get an additional seat at the same time but there is only one seat to give. Answers will vary on fair solutions.
  4. Yes, with a modified divisor of 1200 we get A: 5 seats, B: 5 seats and C: 1 seat.

6.1.10.17.

Solution.
2010: Douglass: 8, Parks: 4, King: 10, Du Bois: 11, Lewis: 17
2020: Douglass: 8, Parks: 5, King: 10, Du Bois: 11, Lewis: 16
The populations in King and Lewis counties grew, but Parks got an extra seat from Lewis. This doesn’t seem fair.

6.1.10.19.

Solution.
  1. Clatsop: 2 counselors, Siletz: 11 counselors
  2. The divisor was 698.38, so 4 new guidance counselors should be hired for Cayuse.
  3. Clatsop: 3 counselors, Siletz: 10 counselors, Cayuse: 4 counselors
  4. Cayuse did get 4 counselors, but one of the counselors from Siletz went to Clatsop. That doesn’t seem fair because their populations didn’t change.

6.2 Voting Methods
6.2.12 Exercises

6.2.12.1.

Solution.
Number of voters 3 3 1 3 2
1st choice A A B B C
2nd choice B C A C A
3rd choice C B C A B

6.2.12.3.

Solution.
  1. There are 47 voters.
  2. A majority is 24 votes.
  3. Atlanta wins the plurality method with 19 votes.
  4. Buffalo wins the Instant Runoff Method with 28 votes.
  5. The points are: Atlanta 94, Buffalo 111 and Chicago 77. Buffalo wins the Borda Count Method.
  6. The points are: Buffalo 2, Atlanta 1. Buffalo wins with Copeland’s method.

6.2.12.5.

Solution.
  1. There are 12 voters.
  2. A majority is 7 votes.
  3. Biology wins the plurality method with 5 votes.
  4. Biology wins the Instant Runoff Method with 7 votes.
  5. The points are: Art 22, Biology 26 and Calculus 24. Biology wins the Borda Count Method.
  6. The points are: Biology 2, Calculus 1. Biology wins with Copeland’s method.

6.2.12.7.

Solution.
  1. There are 31 votes.
  2. A majority is 16 votes.
  3. F wins the plurality method with 12 votes.
  4. E wins the Instant Runoff Method with 16 votes.
  5. The points are: D 66, E 59 and F 61. D wins the Borda Count Method.
  6. The points are: D 2, E 1. D wins with Copeland’s method.

6.2.12.9.

Solution.
  1. There are 460 voters.
  2. A majority is 231 votes.
  3. A wins the plurality method with 150 votes.
  4. A wins the Instant Runoff Method with 290 votes.
  5. The points are: A 1140, B 1060, C 1160 and D 1240. D wins the Borda Count method.
  6. The points are: A 1, B 1, C 2, D 2. C and D tie with Copeland’s method.

6.2.12.11.

Solution.
  1. There are 92 voters.
  2. A majority is 47 votes.
  3. K wins the plurality method with 38 votes.
  4. K wins the Instant Runoff Method with 54 votes.
  5. The points are: I 273, J 152, K 267 and L 228. I wins the Borda Count Method.
  6. The points are: I 2, K 3, L2. K wins with Copeland’s method.

6.2.12.13.

Solution.
  1. There are 90 voters.
  2. A majority is 46 votes.
  3. Q wins the plurality method with 26 votes.
  4. S wins the Instant Runoff Method with 50 votes.
  5. The points are: Q 250, R 201, S 243 and T 206. Q wins the Borda Count Method.
  6. The points are: Q 2, R 1 and S 3. S wins with Copeland’s method.

6.2.12.15.

Solution.
  1. There are 107 voters.
  2. A majority is 54 votes.
  3. E wins the plurality method with 39 votes.
  4. B wins the Instant Runoff Method with 54 votes.
  5. The points are: A 357, B 398, C 305, D 219, E 326. B wins the Borda Count Method.
  6. The points are: A 2, B 4, C 2, D 1, E 1. B wins with Copeland’s method.

6.2.12.17.

Solution.
  1. There are 127 voters.
  2. A majority is 64 votes.
  3. K wins the plurality method with 35 votes.
  4. M wins the Instant Runoff Method with 79 votes.
  5. The points are: K 430, L 402, M 376, N 375, O 322. K wins the Borda Count Method.
  6. The points are: K 4, L 2, M 2, N 2. K wins with Copeland’s method.

6.3 The Popular Vote, Electoral College and Electoral Power
6.3.4 Exercises

6.3.4.1.

Solution.
The president is elected through a process called The Electoral College. States send a certain number of electors, based on their populations, and whichever candidate gets the most votes from these electors becomes president.

6.3.4.3.

Solution.
Two senators represent each state.

6.3.4.5.

Solution.
There are 435 Representatives in the U.S. House of Representatives.

6.3.4.7.

Solution.
  1. State Population Number of
    Representatives    		 Number of
    Senators    		 Number of
    Electors
    Gandhi 450,000 9 2 11
    Mandela 150,000 3 2 5
    Gbowee 600,000 12 2 14
    Total 1,200,000 24 6 30
    This state has 30 electors.
  2. A majority of electoral votes would be 16 votes.

6.3.4.9.

Solution.
  1. State Population Number of
    Representatives    		 Number of
    Senators    		 Number of
    Electors
    Tamez 280,000 7 2 9
    Teters 200,000 5 2 7
    Herrington 400,000 10 2 12
    Osawa 360,000 9 2 11
    Total 1,240,000 31 8 39
    This state has 39 electors.
  2. A majority of electoral votes would be 20 electoral votes.

6.3.4.11.

Solution.
  1. State Votes for
    Candidate A    		 Votes for
    Candidate B    		 Number of Electoral
    Votes for A    		 Number of Electoral
    Votes for B
    Gandhi 216,000 234,000 0 11
    Mandela 37,500 112,500 0 5
    Gbowee 489,450 110,550 14 0
    Total Votes 742,950 457,050 14 16
    A wins the popular vote with 61.9% of the votes.
  2. B wins the electoral college and becomes the president with 53.5% of the electoral votes.

6.3.4.13.

Solution.
  1. State Votes for
    Candidate A    		 Votes for
    Candidate B    		 Number of Electoral
    Votes for A    		 Number of Electoral
    Votes for B
    Tamez 95,480 184,250 0 9
    Teters 104,200 95,800 7 0
    Herrington 203,600 196,400 12 0
    Osawa 46,080 313,920 0 11
    Total Votes 449,360 790,640 19 20
    B wins the popular vote with 63.6% of the vote.
  2. B wins the electoral college and becomes the president with 51% of the electoral votes.

6.3.4.15.

Solution.
  1. State Population Number of
    Representatives    		 Number of
    Senators    		 Number of
    Electors    		 Electoral Votes per
    50,000 people
    Gandhi 450,000 9 2 11 1.22
    Mandela 150,000 3 2 5 1.67
    Gbowee 600,000 12 2 14 1.17
    The state of Mandela has the most electoral power.
  2. The state of Gbowee has the least electoral power.

6.3.4.17.

Solution.
  1. State Population Number of
    Representatives    		 Number of
    Senators    		 Number of
    Electors    		 Electoral Votes per
    50,000 people
    Tamez 280,000 7 2 9 1.29
    Teters 200,000 5 2 7 1.40
    Herrington 400,000 10 2 12 1.20
    Osawa 360,000 9 2 11 1.22
    The state of Teters has the most electoral power.
  2. The state of Herrington has the least electoral power.

6.3.4.19.

Solution.
Possible combinations are Gandhi/Mandela/Gbowee, Gandhi/Mandela, Mandela/Gbowee, or Gandhi/Gbowee. The minimum number of votes needed is 300,002.

6.3.4.21.

Solution.
Possible combinations are Tamez/Teters/Herrington/Osawa, Tamez/Teters/Herrington, Tamez/Teters/Osawa, Tamez/Herrington/Osawa, Teters/Herrington/Osawa, Tamez/Herrington, Tamez/Osawa, or Herrington/Osawa. The minimum number of votes needed is 320,002.

6.4 Gerrymandering and How to Measure It
6.4.5 Exercises

6.4.5.1.

Solution.
Redistricting happens every 10 years after the census is completed. A state might not change its districts unless the number of seats in the U.S. House of Representatives has changed.

6.4.5.3.

Solution.
The rules are districts must be contiguous and you can’t gerrymander by race.

6.4.5.5.

Solution.
The most proportional representation would be 4 Republican seats and 3 Democratic seats.

6.4.5.7.

Solution.
The most proportional representation would be 2 Republican seats and 1 Democratic seat.

6.4.5.9.

Solution.
The most proportional representation would be 6 Republican seats, 4 Democratic seats and 1 Green Party seat.

6.4.5.11.

Solution.
  1. A majority is 4 votes.
  2. The Democrats won 2 seats and the Republicans won 2 seats.
  3. The efficiency gap is \(6/28= 21.43\%\)
    District D Votes R Votes D Surplus Votes R Surplus Vote
    1 1 6 1 \(6-4=2\)
    2 3 4 3 \(4-4=0\)
    3 6 1 \(6-4=2\) 1
    4 7 0 \(7-4=3\) 0
    Total 17 11 9 3
  4. Each seat is worth 25% of the voters.
  5. The efficiency gap is worth less than one seat (0.86 seats).
  6. This map is ok because the efficiency gap is less than one seat. It should either be D3, R1 or D2, R2.

6.4.5.13.

Solution.
  1. A majority is 3 votes.
  2. The Democrats won 1 seat and the Republicans won 4 seats.
  3. The efficiency gap is \(8/25= 32\%\)
    District D Votes R Votes D Surplus Votes R Surplus Vote
    1 2 3 2 \(3-3=0\)
    2 2 3 2 \(3-3=0\)
    3 2 3 2 \(3-3=0\)
    4 4 1 \(4-3=1\) 1
    5 2 3 2 \(3-3=0\)
    Total 12 13 9 1
  4. Each seat is worth 20% of the voters.
  5. The efficiency gap is worth 1.6 seats.
  6. This map is not fair because the efficiency gap is more than one seat. A fairer map would be D3, R2 or D2, R3.

6.4.5.15.

Solution.
  1. A majority is 5 votes.
  2. The Democrats won 2 seats and the Republicans won 3 seats.
  3. The efficiency gap is \(4/45= 8.89\%\)
    District D Votes R Votes D Surplus Votes R Surplus Vote
    1 2 7 2 \(7-5=2\)
    2 5 4 \(5-5=0\) 4
    3 2 7 2 \(7-5=2\)
    4 5 4 \(5-5=0\) 4
    5 4 5 4 \(5-5=0\)
    Total 18 27 8 12
  4. Each seat is worth 20% of the voters.
  5. The efficiency gap is worth less than one seat (0.44).
  6. This map is fair because the efficiency gap is around 8% and the representation is exactly proportional to the population.

6.4.5.17.

Solution.
  1. A majority is 3 votes.
  2. The Democrats won 5 seats and the Republicans won 1 seat.
  3. The efficiency gap is \(12/30= 40\%\)
    District D Votes R Votes D Surplus Votes R Surplus Vote
    1 3 2 \(3-3=0\) 2
    2 3 2 \(3-3=0\) 2
    3 3 2 \(3-3=0\) 2
    4 3 2 \(3-3=0\) 2
    5 3 2 \(3-3=0\) 2
    6 0 5 0 \(5-3=2\)
    Total 15 15 0 12
  4. Each seat is worth 16.67% of the voters.
  5. The efficiency gap is worth 2.4 seats.
  6. This map is not fair because the efficiency gap is more than one seat. A more fair map would be D3, R3 because the population is evenly split.

6.4.5.19.

Solution.
  1. A majority is 5 votes.
  2. The Democrats won 1 seat and the Republicans won 5 seats.
  3. The efficiency gap is \(6/54= 11.11\%\)
    District D Votes R Votes D Surplus Votes R Surplus Vote
    1 2 7 2 \(7-5=2\)
    2 2 7 2 \(7-5=2\)
    3 9 0 \(9-5=4\) 0
    4 2 7 2 \(7-5=2\)
    5 1 8 1 \(8-5=3\)
    6 4 5 4 \(5-5=0\)
    Total 20 34 15 9
  4. Each seat is worth 16.67% of the voters.
  5. The efficiency gap is worth less than 1 seat. (0.67)
  6. This map is not fair because even though the efficiency gap is less than one seat, The Democrats should have at least 2 seats. A more fair map would be D2, R4.

6.4.5.21.

Solution.
  1. The most seats that can be won by the Democrats is 4 seats.
  2. The most seats that can be won by the Republicans is 4 seats.

6.4.5.23.

Solution.
  1. The most seats that can be won by the Democrats is 4 seats.
  2. The most seats that can be won by the Republicans is 5 seats.
PrevTopNext