Savings Plans

Section 3.3 Savings Plans

Objectives: Savings Plans 3.3

Students will be able to:

Use a spreadsheet and/or formula to calculate the future value and interest earned on savings plans
🔗

🔗
Use a spreadsheet and/or formula to calculate payment amounts for savings plans
🔗

🔗
Analyze and compare lump sum and regular payment savings plans
🔗

🔗

For most of us it is not practical to deposit a large sum of money in the bank. Instead, we save by depositing smaller amounts of money regularly. We might save in an IRA or 401-K for retirement. We might also save for a down payment on a car or house, or in a college savings plan for our children.

🔗

Just like the last section, we will emphasize spreadsheets but calculate each example with the formulas as well. Check with your instructor for which way you should do your problems.

🔗

Subsection 3.3.1 Warmup

Preview Activity 3.3.1.

Match the types of graphs with the types of interest below.

🔗

Simple Interest
🔗

🔗
Compound Interest
🔗

🔗

🔗

Preview Activity 3.3.2.

Write the letter of the formula that you would use to solve the problem. Complete the calculation using a spreadsheet.

🔗

Financial Formulas.

A. =P + P*rate*years

🔗

B. =FV(rate, nper, pmt, [pv], [type])

🔗

C. =PV(rate, nper, pmt, [fv], [type])

🔗

D. =P*EXP(rate*years)

🔗

E. =EFFECT(nominal rate, periods per year)

🔗

You deposit $10,000 into an account that earns 5% interest, compounded quarterly, for 20 years.
🔗

🔗
You loan a friend $1,000 for 2 years at 3% simple interest.
🔗

🔗
You want to compare an account that earns 5.4% interest compounded daily with an account that earns 6.2% compounded quarterly.
🔗

🔗
You deposit $7,000 into an account that earns 8% interest compounded continuously for 10 years.
🔗

🔗

🔗

Subsection 3.3.2 Savings Plan Formulas

To make calculations for savings plans using a spreadsheet, we can use the =FV formula we have already used. This time for regular payments we will use the field for payment amount. If we are not making an initial deposit, the present value will be zero.

🔗

Here is the future value formula again:

🔗

Future Value Spreadsheet Formula.

=FV(rate per period, number of periods, payment amount, present value)

🔗

rate per period 🔗: is the interest rate per compounding period, $r/n$
🔗
number of periods 🔗: is the total number of periods, $n*t$
🔗
payment amount 🔗: is the amount of regular payments
🔗
present value 🔗: is the initial principal. If none, enter $0$
🔗

🔗

The mathematical formulas are shown below. If you want to know how we got the formula, it is derived at the end of the chapter.

🔗

Savings Plan Formulas.

\begin{equation*} A=\frac{d\left(\left(1+\frac{r}{n}\right)^{nt}-1\right)}{\left(\frac{r}{n}\right)} \text{ or } d=\frac{A\left(\frac{r}{n}\right)}{\left(\left(1+\frac{r}{n}\right)^{nt}-1\right)} \end{equation*}

🔗

A 🔗: is the balance in the account after n years (future value)
🔗
d 🔗: is the regular deposit (or payment amount each month, quarter, year, etc.)
🔗
r 🔗: is the annual interest rate in decimal form
🔗
n 🔗: is the number of compounding periods in one year
🔗
t 🔗: is the number of years
🔗

🔗

If the compounding frequency is not explicitly stated, assume there are the same number of compounds in a year as there are deposits made in a year.

🔗

If you make your deposits every year, use yearly compounding, $n=1\text{.}$

🔗

If you make your deposits every quarter, use quarterly compounding, $n=4\text{.}$

🔗

If you make your deposits every month, use monthly compounding, $n=12\text{,}$ etc.

🔗

To see how both of these methods work, let’s look at an example.

🔗

Example 3.3.1.

A traditional individual retirement account (IRA) is a special type of retirement account in which the money you invest is exempt from income taxes until you withdraw it. If you deposit $100 each month into an IRA earning 6% APR, how much will you have in the account after 20 years? How much will you have earned in interest? What percentage of the balance is interest?

🔗

Solution.

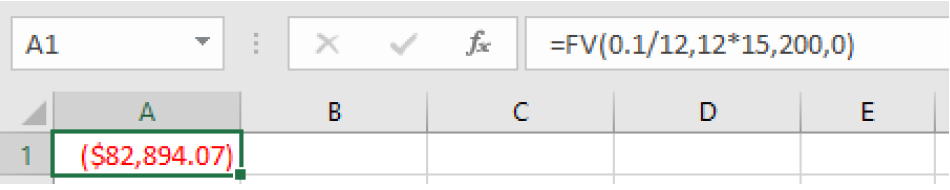
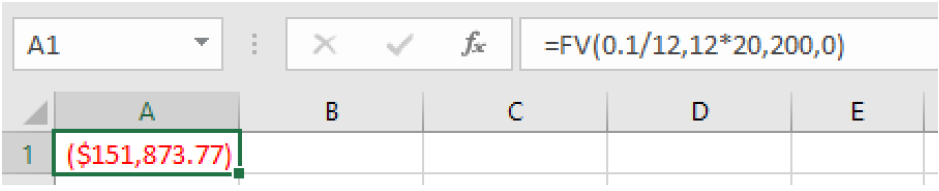
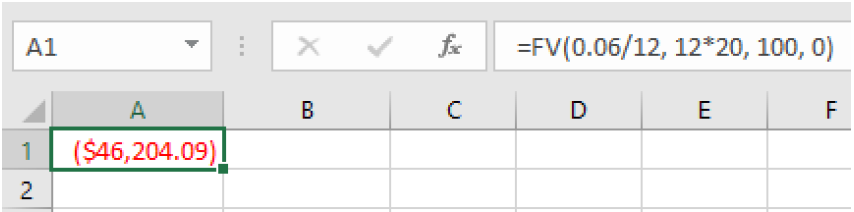
To use a spreadsheet, we will use =FV because we want to know the balance in the future. We enter 100 for the payment amount and 0 for the present value:

🔗

=FV(0.06/12, 12*20, 100, 0)

🔗

which gives a result of $46,204.09.

🔗

An image of the spreadsheet showing the formula used and the result.

Remember that the output of the formula gives the answer with the opposite sign as the principal and payments. For our purposes we will ignore the signs. To use the formula, we use the one solved for A, since we want to know the final amount.

🔗

$d=\$100\text{,}$ the monthly deposit

🔗

$r=0.06\text{,}$ 6% annual rate

🔗

$n=12\text{,}$ since we’re doing monthly deposits, we’ll compound monthly

🔗

$t=20\text{,}$ we want the amount after 20 years

🔗

Putting this into the equation we have:

🔗

\begin{align*} A\amp=\frac{100\left(\left(1+\frac{0.06}{12}\right)^{12\cdot 20}-1\right)}{\left(\frac{0.06}{12}\right)}\\ \amp=\frac{100\left((1.005)^{240}-1\right)}{(0.005)}\\ \amp\approx \$46.204.09 \end{align*}

🔗

With U.S. dollars we round to the nearest cent. The account will grow to $46,204.09 after 20 years.

🔗

To find the amount of interest earned, calculate the total of all your deposits.

🔗

\begin{equation*} \$100(20)(12)=\$24,000 \end{equation*}

🔗

The difference between the total amount and the deposits is the interest earned.

🔗

\begin{equation*} \$46,204.09-\$24,000=\$22,204.09 \end{equation*}

🔗

The total amount of interest you earned was $22,204.09.

🔗

To find the percentage of the balance that is interest we will divide the interest by the total balance.

🔗

\begin{equation*} \frac{\$22,204.09}{\$46,204.09}\approx 0.4810 \end{equation*}

🔗

or 48.1%. After 20 years 48.1% of the balance is from interest.

🔗

Now here’s an example with an initial deposit and monthly deposits. We can do this with the spreadsheet formula.

🔗

Example 3.3.2.

You want to jumpstart your saving by depositing $1500 from your tax return and then deposit $150 every month into an account that earns 5.5% APR compounded monthly. How much will you have in the account after 30 years?

🔗

Solution.

Using the spreadsheet formula, we can enter an initial deposit and a monthly payment. We enter

🔗

=FV(0.055/12, 12*30, 150,1500)

🔗

and get a result of $144,822.87.

🔗

Subsection 3.3.3 Finding Payment Amounts Usings Spreadsheets and Formulas

Another important thing we can calculate is how much we need to save in each period to have a specified amount in the future. Say you want to achieve a certain amount for retirement or for your kids’ college.

🔗

The mathematical formula for this is the one solved for d, the payment amount, above. There is a new spreadsheet formula to calculate payments, =PMT, that we will introduce now.

🔗

Payment Spreadsheet Formula.

=PMT(rate per period, number of periods, present value, future value)

🔗

rate per period 🔗: is the interest rate per compounding period, $r/n$
🔗
number of periods 🔗: is the total number of periods, $n*t$
🔗
present value 🔗: is the amount deposited or principal, $P$
🔗
future value 🔗: is the amount you want in the future, $A$
🔗

🔗

Here is an example of a retirement goal calculated with a spreadsheet and the formula.

🔗

Example 3.3.3.

You want to have half a million dollars in your account when you retire in 30 years. Your retirement account earns 8% APR. How much do you need to deposit each month to meet your retirement goal?

🔗

Solution.

To calculate this with a spreadsheet, we will use the =PMT function and enter 0 for the present value and $500,000 for the future value. We cannot enter commas within the numbers however, because spreadsheets use commas to separate the inputs. We enter:

🔗

=PMT(0.08/12, 12*30, 0, 500000)

🔗

and get a result of $335.49.

🔗

To see how this works with the formulas, we use the one solved for d, the regular deposit amount.

🔗

$r=0.08\text{,}$ 8% annual rate

🔗

$n=12\text{,}$ since we’re depositing monthly

🔗

$t=30\text{,}$ 30 years

🔗

$A=\$500,000\text{,}$ the amount we want to have in 30 years

🔗

\begin{align*} d\amp=\frac{A\left(\frac{r}{n}\right)}{\left(\left(1+\frac{r}{n}\right)^{nt}-1\right)}\\ \amp=\frac{500000\left(\frac{0.08}{12}\right)}{\left(\left(1+\frac{0.08}{12}\right)^{12\cdot 30}-1\right)}\\ \amp\approx\$335.49 \end{align*}

🔗

So, you would need to deposit $335.49 each month to have $500,000 in 30 years if your account earns 8% interest.

🔗

Activity 3.3.3.

Use a spreadsheet to work on these problems. Write down the syntax to show your work. Answer each question in a complete sentence.

🔗

Jackie is 34 years old. She would like to have one million dollars in her retirement account when she is 65 years old.

🔗

How much would she need to deposit every month into an account with an APR of 7.25%, compounded monthly, to achieve her goal?
🔗

🔗
If Jackie had started the account at age 21 (same APR), how much would she need to deposit every month to achieve her goal?
🔗

🔗
If Jackie had started the account at age 21 (same APR) and deposited the amount calculated in Exercise 1 every month, what would the balance be when she retired at age 65?
🔗

🔗
How much would Jackie need to deposit as a lump sum at age 21 with the same APR (without making another payment) to have a million dollars at age 65?
🔗

🔗

🔗

A note about rounding.

If you are using the formulas and round during intermediate steps you will probably have some roundoff error. For this reason, we enter the whole expression into the calculator and do not show the intermediate steps.

🔗

One of the challenges in this chapter is choosing the correct formula or spreadsheet function. Read this next example and see if you can determine which formula to use.

🔗

Example 3.3.4.

A more conservative investment account pays 3% APR. If you deposit $5 a day into this account, how much will you have after 10 years? What amount and percentage are from interest?

🔗

Solution.

In this example we are given the regular deposit amount and we are looking for the future value. In a spreadsheet we use the =FV function and enter:

🔗

=FV(0.03/365, 365*10, 5,0)

🔗

which gives a result of $21,282.07.

🔗

To use a mathematical formula, we choose the one solved for A:

🔗

$d=\$5\text{,}$ the daily deposit

🔗

$r=0.03\text{,}$ 3% annual rate

🔗

$n=365\text{,}$ since we’re doing daily deposits, we’ll compound daily

🔗

$t=10\text{,}$ we want the amount after 10 years

🔗

\begin{align*} A\amp=\frac{5\left(\left(1+\frac{0.03}{365}\right)^{365\cdot 10}-1\right)}{\left(\frac{0.03}{365}\right)}\\ \amp\approx\$21,282.07 \end{align*}

🔗

To find the amount of interest, we will calculate how much was deposited in the account. Since you put in $5 a day for 10 years we get

🔗

\begin{equation*} \$5(365)(10)=\$18,250\text{.} \end{equation*}

🔗

The interest earned is $\$21,282.07-\$18,250=\$3,032.07\text{.}$

🔗

To find the percentage we divide by the total balance to get $\frac{\$3,032.07}{\$21,282.07}\approx0.1425$ or 14.25%.

🔗

After 10 years, about 14.25% of the account is interest.

🔗

Subsection 3.3.4 Comparing Lump Sum and Regular Savings Payments

Now let’s compare two scenarios to do some multistep problems and get a sense for the value of compounding over time.

🔗

Example 3.3.5.

Scenario 1: Suppose you invest $200 a month for 15 years into an account earning 10% APR compounded monthly. After 15 years, you leave the money, without making additional deposits, in the account for another 20 years. How much will you have in the end?

🔗

Scenario 2: Suppose instead you didn’t invest anything for the first 15 years, then deposited $200 a month for 20 years into an account earning 10% APR compounded monthly. How much will you have in the end?

🔗

Solution.

Before we calculate the balance for both scenarios, which one do you think will have a higher balance at the end?

🔗

For scenario 1, there are two steps involved. The first part is the monthly payments for 15 years. To calculate this with a spreadsheet we enter

🔗

=FV(0.10/12, 12*15, 200,0)

🔗

which gives $82,894.07.

🔗

Now you will stop making payments and let the money sit and earn interest for 20 more years. With a spreadsheet we enter

🔗

=FV(0.10/12, 12*20, 0, 82894.07)

🔗

which gives $607,453.85.

🔗

The process is similar with the formulas. For the first step we have:

🔗

\begin{align*} A\amp=\frac{200\left(\left(1+\frac{0.10}{12}\right)^{12\cdot 15}-1\right)}{\left(\frac{0.10}{12}\right)}\\ \amp\approx\$82,894.07 \end{align*}

🔗

And for the second step we use the compound interest formula from Section 3.2.

🔗

\begin{align*} A\amp=\$82,894.07\left(1+\frac{0.10}{12}\right)^{12\cdot 20}\\ \amp\approx\$607,453.85 \end{align*}

🔗

Now for Scenario 2: Since we are not investing anything for the first 15 years there is nothing to calculate. This is a one-step problem. We will find the future value with the monthly payments of $200 for 20 years. With a spreadsheet we enter

🔗

=FV(0.10/12, 12*20, 200,0)

🔗

which gives $151,873.77.

🔗

To check that with the formula we have:

🔗

\begin{align*} A\amp=\frac{200\left(\left(1+\frac{0.10}{12}\right)^{12\cdot 20}-1\right)}{\left(\frac{0.10}{12}\right)}\\ \amp\approx\$151,873.77 \end{align*}

🔗

Were you surprised by these numbers? You would put in less money in scenario 1 and end up with four times as much. The key to compounding interest is to start early. If you remember the graph of compound interest in Section 3.2, we can see that as time goes on, the balance increases exponentially.

🔗

Activity 3.3.4. Sal, Cal, and Val.

Sal, Cal and Val are triplets.

Sal gets a paper route at age 14 and decides to invest $150 each month in a mutual fund which averages a 10% annual return. Sal only makes deposits for 5 years and then leaves the balance to compound until retirement at age 65.
🔗

🔗
Cal is impressed by Sal’s bank account, and gets a job in college at age 19 and dutifully makes deposits of $150 each month into the same mutual fund for 9 years and then leaves the balance to compound until retirement at age 65.
🔗

🔗
Val partied a lot growing up, but then gets a good job at the age of 27 and diligently makes deposits of $150 each month all the way to retirement at the age of 65.
🔗

🔗

🔗

Answer the following questions:

🔗

How much money did each brother invest?
🔗

🔗
How much does each brother have saved for retirement at age 65?
🔗

🔗
Put the interest rate of 10% into a cell in your spreadsheet, then redo your formulas for Item b so that they reference this cell. Try changing the interest rate until Sal and Cal end up with the same amount at age 65. What is this interest rate?
🔗

🔗
What interest rate causes Cal and Val to end up with the same amount at age 65?
🔗

🔗

🔗

Subsection 3.3.5 Deriving the Savings Plan Formula (Optional)

If you are interested in where the savings plan formula came from, we will explain it here. A savings plan with regular payments can be described recursively. Recall that basic compound interest follows from the relationship for each compound period.

🔗

$A=P\left(1+\frac{r}{n}\right)$

🔗

For a savings plan, we need to add a deposit, d, to the account with each compounding period:

🔗

$A=P\left(1+\frac{r}{n}\right)+d$

🔗

Taking this equation from recursive form to explicit form is a bit trickier than with compound interest. It will be easiest to see by working with an example rather than working in general.

🔗

Suppose we will deposit $100 each month into an account paying 6% APR. We assume that the account is compounded with the same frequency as we make deposits unless stated otherwise.

🔗

In this example:

🔗

$r=0.06\text{,}$ 6% APR

🔗

$n=12\text{,}$ 12 compounds/deposits per year

🔗

$d=\$100\text{,}$ our deposit per month

🔗

Writing out the recursive equation gives where A is exchanged with $P_{m}$ where m is the number of compounding periods.

🔗

$P_{m}=\left(1+\frac{0.06}{12}\right)P_{m-1}+100=(1.005)P_{m-1}+100$

🔗

Assuming we start with an empty account, we can begin using this relationship:

🔗

$P_{0}=0$

🔗

$P_{1}=(1.005)P_{0}+100=100$

🔗

$P_{2}=(1.005)P_{1}+100=(1.005)(100)+100=100(1.005)+100$

🔗

$P_{3}=(1.005)P_{2}+100=(1.005)(100(1.005)+100)+100=100(1.005)^{2}+100(1.005)+100$

🔗

Continuing this pattern, after m deposits, we’d have saved:

🔗

$P_{m}=100(1.005)^{m-1}+100(1.005)^{m-2}+...+100(1.005)+100$

🔗

In other words, after $m$ months, the first deposit will have earned compound interest for $m-1$ months. The second deposit will have earned interest for $m-2$ months. Last month’s deposit would have earned only one month worth of interest. The most recent deposit will have earned no interest yet.

🔗

This equation leaves a lot to be desired, though – it doesn’t make calculating the ending balance any easier! To simplify things, multiply both sides of the equation by 1.005:

🔗

$1.005P_{m}=1.005[100(1.005)^{m-1}+100(1.005)^{m-2}+...+100(1.005)+100]$

🔗

Distributing on the right side of the equation gives

🔗

$1.005P_{m}=100(1.005)^{m}+100(1.005)^{m-1}+...+100(1.005)^{2}+100(1.005)$

🔗

Now we’ll line this up with like terms from our original equation, and subtract each side

🔗

$1.005P_{m}=100(1.005)^{m}+100(1.005)^{m-1}+...+ 100(1.005)$

🔗

$P_{m} = 100(1.005)^{m-1}+...+ 100(1.005)+100$

🔗

Almost all the terms cancel on the right side when we subtract, leaving

🔗

$1.005P_{m}-P_{m}=100(1.005)^{m}-100$

🔗

Solving for $P_{m}$

🔗

$0.005P_{m}=100((1.005)^{m}-1)$

🔗

$P_{m}=\frac{100(1.005)^{m}-100}{0.005}$

🔗

Replacing $P_{m}$ with $A$ (Future Value), $m$ months with $12t\text{,}$ where $t$ is measured in years, gives

🔗

$A=\frac{100(1.005)^{12t}-1}{0.005}$

🔗

Recall $0.005$ was $r/n$ and 100 was the deposit $d\text{.}$ The value 12 as $n\text{,}$ the number of deposits each year. Generalizing this result, we get the savings plan formula solved for $A\text{.}$ The second formula uses algebra to rearrange the formula to be solved for $d\text{.}$

🔗

Savings Plan Formulas.

🔗

A 🔗: is the balance in the account after n years (future value)
🔗
d 🔗: is the regular deposit (or payment amount each month, quarter, year, etc.)
🔗
r 🔗: is the annual interest rate in decimal form
🔗
n 🔗: is the number of compounding periods in one year
🔗
t 🔗: is the number of years
🔗

🔗

If the compounding frequency is not explicitly stated, assume there are the same number of compounds in a year as there are deposits made in a year

🔗

Exercises 3.3.6 Exercises

1.

You set up a savings plan for retirement in 35 years. You will deposit $250 each month for 35 years. The account will earn an average of 6.5% APR compounded monthly.

How much will you have in your retirement plan in 35 years?
🔗

🔗
How much interest did you earn.
🔗

🔗
What percent of the balance is interest?
🔗

🔗

🔗

2.

You set up a savings plan for retirement in 40 years. You will deposit $75 each week for 40 years.The account will earn an average of 8.5% APR compounded weekly.

How much will you have in your retirement plan in 40 years?
🔗

🔗
How much interest did you earn.
🔗

🔗
What percent of the balance is interest?
🔗

🔗

🔗

3.

You set up a savings plan for retirement in 30 years. You will deposit $750 each quarter for 30 years. The account will earn an average of 7.75% APR compounded quarterly.

How much will you have in your retirement plan in 30 years?
🔗

🔗
How much interest did you earn?
🔗

🔗
What percent of the balance is interest?
🔗

🔗

🔗

4.

You set up a savings plan for retirement in 25 years. You will deposit $20 per day for 25 years. The account will earn an average of 2.35% APR compounded daily.

How much will you have in your retirement plan in 25 years?
🔗

🔗
How much interest did you earn?
🔗

🔗
What percent of the final balance is interest?
🔗

🔗

🔗

5.

Suppose you invest $130 a month for 5 years into an account earning 9% APR compounded monthly. After 5 years, you leave the money, without making additional deposits, in the account for another 25 years.

How much will you have in the end?
🔗

🔗
How much interest did you earn?
🔗

🔗
What percent of balance is interest?
🔗

🔗

🔗

6.

Suppose you invest $200 per month for 10 years into an account earning 5% APR compounded monthly. You then leave the money, without making additional deposits, in the account for another 20 years.

How much will you have after the first 10 years?
🔗

🔗
How much will you have after the additional 20 years?
🔗

🔗
How much total interest did you earn?
🔗

🔗
What percent of the final balance is interest?
🔗

🔗

🔗

7.

Suppose you have 30 months in which to save $3,500 for a cruise for your family. If you can earn an APR of 3.8%, compounded monthly, how much should you deposit each month?

🔗

8.

You wish to have $3,000 in 2 years to buy a fancy new stereo system. How much should you deposit each quarter into an account paying 6.5% APR compounded quarterly?

🔗

9.

Jamie has determined they need to have $450,000 for retirement in 30 years. Their account earns 6% APR. How much would Jamie need to deposit in the account each month?

🔗

10.

Lashonda already knows that she wants $500,000 when she retires. If she sets up a saving plan for 40 years in an account paying 10% APR, compounded quarterly, how much should she deposit each quarter?

🔗

11.

Jose’ inherits $55,000 and decides to put it in the bank for the next 25 years to save for his retirement. He will earn an average of 5.6% APR compounded monthly for the next 25 years. His partner deposits $375 a month in a separate savings plan that earns 5.6% APR compounded monthly for the next 25 years.

How much will each have at the end of 25 years?
🔗

🔗
How much interest did each person earn?
🔗

🔗
What percent of balance is interest for each person?
🔗

🔗

🔗

12.

Akiko inherits $45,000 and decides to put it in the bank for the next 30 years to save for her retirement. She will earn an average of 7.8% APR compounded monthly for the next 30 years. Her spouse deposits $200 a month in a separate savings plan that earns 7.8% APR compounded monthly for the next 30 years.

How much will each have at the end of 30 years?
🔗

🔗
How much interest did each person earn?
🔗

🔗
What percent of balance is interest for each person?
🔗

🔗

🔗

13.

Sylvin makes an initial deposit of $1000 into a savings account and then adds $100 each month for 10 years into an account pays 4.5% APR compounded monthly.

What will be her final balance?
🔗

🔗
How much interest did she earn?
🔗

🔗
What percent of the final balance is interest?
🔗

🔗

🔗

14.

Elena makes an initial deposit of $5000 into a savings account and then adds $1000 each year for 20 years into an account pays 2.35% APR compounded annually.

What will be her final balance?
🔗

🔗
How much interest did she earn?
🔗

🔗
What percent of her final balance is interest?
🔗

🔗

🔗

15.

Vanessa just turned 40 years old. Her plan is to save $100 per month until retirement at age 65. Suppose she deposits that $100 each month into a savings account that earns 4% APR compounded monthly.

What will her balance be when she turns 65 years old?
🔗

🔗
If she started saving when she turned 25 years old instead, what would her balance be?
🔗

🔗

🔗

16.

Chris wants to start saving money for retirement. Suppose he deposits $1000 every year into a savings account that pays 5% APR compounded annually.

How much will Chris have saved in 20 years?
🔗

🔗
How much will Chris have saved in 40 years?
🔗

🔗

🔗

17.

Fareshta and Ahmad want to save to help send their child to college. Their plan is to put aside $50 every week. Suppose they deposit that money into an account that pays 3.5% APR compounded weekly.

How much money will be in the account in 18 years? (assume 52 weeks in a year)
🔗

🔗
What minimum initial lump sum deposit would they need to make today to have the same balance in 18 years if they weren’t putting aside the $50 per week?
🔗

🔗

🔗

18.

Elisa decides to cancel her cable TV and to deposit the $100 she will save each month into an account that pays 4.5% APR compounded monthly.

How much will she have in the account in 10 years?
🔗

🔗
What minimum initial lump sum deposit would she need to make today to have the same balance in 10 years without saving the $100 per month?
🔗

🔗

🔗

Prev Top Next