Section 6.3 The Popular Vote, Electoral College and Electoral Power
Objectives: Section 6.3
Students will be able to:
Calculate the number of electors per state
Determine the winner of the popular vote
Determine the winner of the electoral college
Calculate the electoral power of each state
Subsection 6.3.1 Choosing the U.S. President
In the last section we talked about equal voting rights and studied several voting methods. To choose the President of the United States, we use another method, called the Electoral College. The Founders, with their newfound freedom from Britain, wanted to create a democracy where citizens could participate in choosing their president. Prior to the Electoral College, there were three options proposed (Best, 2004; Clayton, 2015). They were
Congress would elect the president
State Legislatures would vote and elect the president
The people would elect a president by popular vote
The first option of having Congress do this work was declined as this would alter the balance of power among the three separate branches of government. The idea to have State Legislatures also failed as there wouldn’t be the separation between having an independent Federal Government and State Governments.
The popular vote means a candidate must win a plurality of all the votes cast for president, regardless of which state the voters live in. The popular vote was decided against as the Founders didn’t think all citizens would be informed enough about the candidates to make an educated decision (Clayton, 2015).
Instead, the Electoral College was decided upon and, in this system, each state was given a certain number of electoral votes. Each state got an equal two votes for the two senate seats. This gave smaller states a leg up as they would have at least these votes. In addition, each state would be given more votes based on their population, equal to their representation in the House (Clayton, 2015). The District of Columbia, which is not a state, also gets 3 electoral votes. A candidate must win a majority of the electoral votes to win the U.S. presidency. If no candidate has a majority of electoral votes then a contingent election would be held by the U.S. House of Representatives between the three candidates with the most electoral votes.
The 4 million U.S. Citizens who live in the U.S. territories of Guam, the Virgin Islands, the Northern Mariana Islands and Puerto Rico cannot vote in the presidential elections and do not have any electors for the U.S. President. Additionally, there are U.S. Nationals in American Samoa and other territories that cannot vote. You can learn more about residents of these territories in this Census Bureau Report 78 . We will also reiterate that voter suppression still exists and elections will not be truly fair until all of its forms are eliminated.
As stated in the Constitution, the U.S. currently has 435 representatives in the House. They each serve 2-year terms, while the two senators from each state serve 6-year terms.
Example 6.3.2.
How many electoral votes are there in the U.S. Electoral College?
\(100+435+3=538\)
By adding all the U.S. Senators, Representatives and 3 for Washington, D.C., we have a total of 538 electoral votes.
Example 6.3.3.
How many electoral votes does a candidate need to win to become the President of the United States?
\(538\div2=269\) then round up to 270.
A candidate needs 270 electoral votes to win the U.S. Presidency.
Example 6.3.4.
The number of people who voted in the presidential election in 2016 was 136,452,150 (Ballotpedia, n.d.). How many votes would be needed to win a majority of the popular vote?
\(136,452,150\div2=68,226,075\) then round up to 68,226,076.
A candidate would need 68,226,076 votes to win the popular vote.
Example 6.3.5.
There were approximately 230,931,921 eligible voters at the time of the 2016 election (McDonald, 2016). What percentage of eligible voters voted?
\(136,452,150 \div 230,931,921 = 0.591\)
About 59% of all the eligible voters voted in the 2016 election.
If you are interested in the 2016 election voting rates by race, Hispanic origin and age, you can find them in this Census Bureau Report 79 .
Subsection 6.3.2 How Electoral Votes are Determined
While each state has a set number of electoral votes based on the formula above, the federal government gave states the control of how they distribute and cast their electoral votes (Paiva, 2011). In 48 states, the candidate with the most votes wins all of that state’s electoral votes, often called winner-takes-all. In essence, a candidate could win with barely a majority of the popular vote in that state and the entire state’s votes goes to that individual (Clayton, 2015). In 2 states, Maine and Nebraska, however, they use a district plan where instead of winner-takes-all, they use proportionality. This means that they award electoral votes by how individual districts vote. Each district gives their electoral vote to the winner of their district and the remaining two votes go to the candidate that won statewide.
There is a movement to change from the Electoral College to the popular vote. One way this is happening is through the National Popular Vote Interstate Compact 80 . States who adopt this compact agree to award their electoral votes to the winner of the national popular vote. If states and/or D.C. with at least 270 electoral votes adopt this compact, then the winner of the popular vote would win the electoral college and the presidency. At this time there are 196 electoral votes in states and D.C. who have enacted the bill and the bill has passed one or two legislative houses in additional states with 88 electoral votes.
After citizens cast their votes by mail or on election day on the first Tuesday in November, electors gather in December and are responsible for casting the votes for their state. Electors cannot be elected officials and are chosen by their parties. Electors are expected to vote in alignment with the state they represent, but there have been faithless electors in the past. The U.S. Supreme Court ruled in July of 2020 that states can penalize electors who do not vote according to the law of the state.
To see how the electoral college and popular votes work, we will look at a made-up country with a smaller number of states.
Example 6.3.6.
Consider this country with 4 states. The rules for the number of senators and electors are the same as the U.S. government. Each state will get 1 representative for every 40,000 residents. For simplicity we will ignore any remainders.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
|---|---|---|---|---|
| Small | 154,600 | |||
| Medium | 262,340 | |||
| Large | 581,135 | |||
| Huge | 1,362,070 |
Determine the number of electors for each state and the total for the country.
How many electoral votes are needed to win the presidential election?
Determine which candidate wins the popular vote and the electoral college vote.
Write down all the possible combinations of states that would win the election based on the electoral college.
What is the fewest number of individual votes needed to win the Electoral College?
What is the smallest percentage of the population that you can win the Electoral College with?
-
To find the number of electors for each state, we first divide each state population by 40,000 to determine the number of representatives they will have. We will drop the decimal remainders, similar to Hamilton’s method.
State Population Number of
RepresentativesNumber of
SenatorsNumber of
ElectorsSmall 154,600 \(154,600 \div 40,000= 3.865 \rightarrow 3\) Medium 262,340 \(262,340 \div 40,000= 6.559 \rightarrow 6\) Large 581,135 \(581,135 \div 40,000= 14.528 \rightarrow 14\) Huge 1,362,070 \(862,070 \div 40,000= 21.552 \rightarrow 21\) State Population Number of
RepresentativesNumber of
SenatorsNumber of
ElectorsSmall 154,600 3 2 Medium 262,340 6 2 Large 581,135 14 2 Huge 1,362,070 21 2 Then we will add the number of representatives and the senators for each state.
State Population Number of
RepresentativesNumber of
SenatorsNumber of
ElectorsSmall 154,600 3 2 5 Medium 262,340 6 2 8 Large 581,135 14 2 16 Huge 1,362,070 21 2 23 Totals 1,860,145 44 8 52 Now we can add up the total of all the electors from each state and we have:
\(5 + 8 + 16 + 23 = 52\) electors.
-
To find out how many electoral votes are needed to win the presidential election, we calculate a majority of 52 electors.
\(52 \div 2 = 26\text{,}\) round up to 27
27 electoral votes are needed to win the presidential election in this state
-
To find the winner for each method, we need the results of an election. In our example, there are 2 candidates for the president, Candidate A and Candidate B. When a candidate wins in a state, they get all the electoral votes for that state. Given the votes for each candidate below, determine who wins the popular vote and who wins the electoral college vote.
State Votes for
Candidate AVotes for
Candidate BNumber of Electoral
Votes for ANumber of Electoral
Votes for BSmall 56,259 98,341 Medium 130,082 132,258 Large 278,177 302,958 Huge 546,555 315,515 Totals First, we will add up all the votes for each candidate in their columns. Next, we will look at each state individually to determine which candidate wins each state. Candidate B has more votes in Small, Medium and Large, so Candidate B gets all of the electoral votes in those states. Candidate A won Huge, so they get all of those electoral votes. We enter zero for the candidate who does not win in each state. Then we add up the electoral vote columns. Here is the completed table.
State Votes for
Candidate AVotes for
Candidate BNumber of Electoral
Votes for ANumber of Electoral
Votes for BSmall 56,259 98,341 0 5 Medium 130,082 132,258 0 8 Large 278,177 302,958 0 16 Huge 546,555 315,515 23 0 Totals 1,011,073 849,072 23 29 Now we can see that Candidate A wins the popular vote with 1,011,073 votes compared to 849,072 for Candidate B. But Candidate B wins the Electoral College with 29 electoral votes. So, Candidate B becomes the President of the United States.
There have been 5 U.S. presidential elections where the winner of the popular vote was not the winner of the electoral college. In all the other elections, the two methods agreed and would have elected the same candidate.
Try calculating the results if these were the votes instead:
State Votes for
Candidate AVotes for
Candidate BNumber of Electoral
Votes for ANumber of Electoral
Votes for BSmall 56,259 98,341 Medium 131,200 131,140 Large 278,177 302,958 Huge 546,555 315,515 Totals State Votes for
Candidate AVotes for
Candidate BNumber of Electoral
Votes for ANumber of Electoral
Votes for BSmall 56,259 98,341 0 5 Medium 131,200 131,140 8 0 Large 278,177 302,958 0 16 Huge 546,555 315,515 23 0 Totals 1,012,191 847,954 31 21 This time Candidate A won Medium and Huge. That gave them the electoral vote victory. Note that the race in Medium was very close, and we only changed 1,118 votes or 0.06% of the votes to Candidate A which gave them the Electoral College.
Opponents of the Electoral College system say that it causes candidates to focus on a few swing states, rather than campaigning equally in all states.
-
Let’s look at which combinations of states the candidates could seek to win with.
Since 27 electoral votes are needed, we will list all the winning combinations starting with the smallest number of states to win. We see that a candidate must win either Huge or Large, because Small and Medium together are not enough votes to win
Combination Small, 5 Medium, 8 Large, 16 Huge, 23 Total Huge + Small 5 23 28 Huge + Medium 8 23 31 Huge + Large 16 23 39 Huge + Small + Medium 5 8 23 36 Huge + Medium + Large 8 16 23 47 Huge + Small + Large 5 16 23 44 Large + Small + Medium 5 8 16 29 All States 5 8 16 23 52 From the table we find there are 8 different ways to win the electoral college and candidates should definitely campaign in Large and Huge.
-
To find the fewest number of individual votes a candidate could win with; let’s look at the table above. The combination of states with the fewest electoral votes is Huge and Small. Let’s see how many votes would be needed to win those two states.
For Huge:
\(862,070 \div 2 = 431,035\text{,}\) then round up to 431,036
For Small:
\(154,600 \div 2 = 77,300\text{,}\) then round up to 77,301
\(431,036+77,301 \text{ votes } = 508,337 \text{ votes}\)
-
The smallest number of votes to win the electoral college is 508,337. What percentage of the population is that? We will divide by the total population to get
\(508,337 \div 1,860,145 = 0.2733\)
If a candidate had the right combination of states, they could win the Electoral College with only 27.3% of the vote.
People who support the Electoral College often say it protects small states. People who oppose the Electoral College often say that each person’s vote should count equally as in the popular vote. Next we will look at electoral power to understand the effect on small states.
People who support the Electoral College often say it protects small states. People who oppose the Electoral College often say that each person’s vote should count equally as in the popular vote. Next we will look at electoral power to understand the effect on small states.
Subsection 6.3.3 Electoral Power
Electoral power is the value of a person’s vote in one state compared to another state. A related topic is voting power, which is the probability of any one person influencing an election. If you are interested in voting power, you can look up the Banzhaf Power Index. To calculate the electoral power, we will calculate a ratio of electoral votes for a given number of people. We could use any number, so we will choose the number of people that each representative represents, which is our divisor of 40,000 people.
Example 6.3.7.
Using the same fictional country, use the table below to calculate the electoral power of each state.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
Electoral Votes Per 40,000 people |
|---|---|---|---|---|---|
| Small | 154,600 | ||||
| Medium | 262,340 | ||||
| Large | 581,135 | ||||
| Huge | 1,362,070 |
First, we fill in the number of representatives, senators and electoral votes for each state that we found earlier. Then we will calculate the number of electoral votes per 40,000 people.
To do that, divide the number of electors by the number of representatives, since they each represent approximately 40,000 people. The results are shown in the table below. Note this is approximate because we cut off the decimal remainders when calculating the number of representatives.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
Electoral Votes Per 40,000 people |
|---|---|---|---|---|---|
| Small | 154,600 | 3 | 2 | 5 | \(5\div3 \approx 1.67\) |
| Medium | 262,340 | 6 | 2 | 8 | \(8\div6 \approx 1.33\) |
| Large | 581,135 | 14 | 2 | 16 | \(16 \div14 \approx 1.14\) |
| Huge | 1,362,070 | 21 | 2 | 23 | \(23\div21 \approx 1.10\) |
Are you surprised to see that the smallest states have the highest electoral power? That is part of the design of the electoral college. The founders from small states were concerned that their votes would not matter, so every state gets 2 senators added to the number of representatives. For a state with few representatives, those 2 extra electoral votes make a big difference. For a large states, the extra 2 electoral votes don’t make a very big difference.
You may have noticed a pattern when dividing to find the electoral power. Each time we divided the number of electoral votes by that number minus two. We can write that pattern as \(\frac{n}{n-2}\text{.}\) Using GeoGebra to graph that pattern this is what we see.
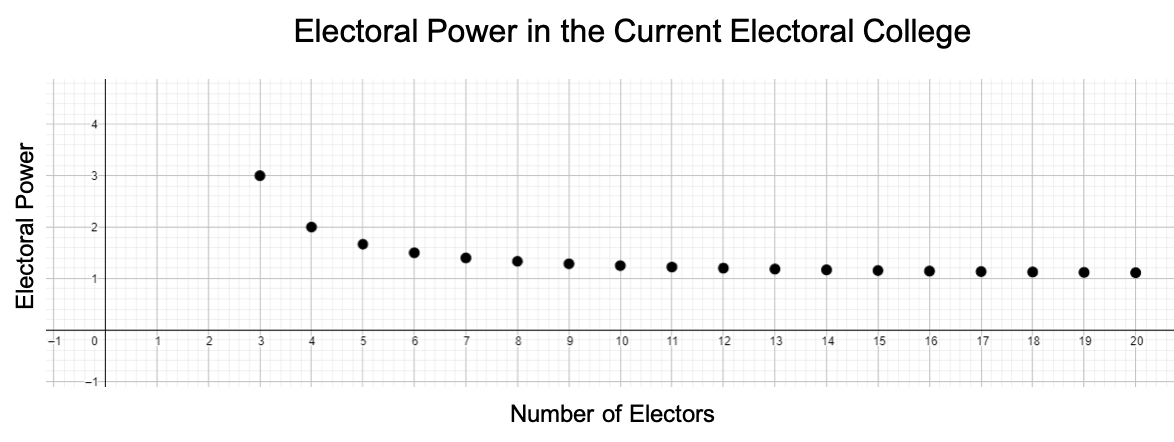
The minimum number of electors is three, since each state gets at least one representative in the apportionment process. The smallest states and Washington, D.C. have 3 electors and the greatest electoral power on the left side of the graph. The largest states like California, Florida and Texas have the least electoral power on the right side of the graph.
Let’s say instead each state had equal electoral power by removing the 2 extra electoral votes or by using the popular vote. Then the graph would look like this.
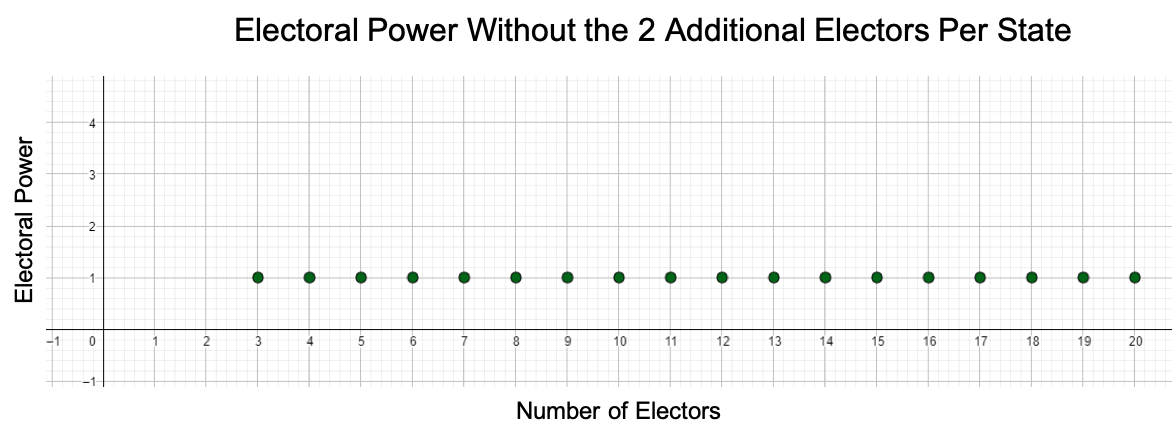
Now that we have studied the popular vote, the Electoral College and electoral power, we leave it up to you to choose which method you think is best.
Exercises 6.3.4 Exercises
1.
How is the U.S. President selected?
2.
How many electors are there in the U.S. Electoral College?
3.
How many U.S. Senators represent each state?
4.
What is the length of a term of a U.S. Senator?
5.
How many Representatives serve in the U.S. House of Representatives?
6.
What is the length of a term of a U.S. Representative?
Exercise Group.
In each fictional country in problems 7-10, use the rules of the U.S. government to complete the table and determine the following:
The total number of electors in the state.
The number of electoral votes needed for a majority and win a presidential election.
7.
In this country there is one representative for every 50,000 residents.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
|---|---|---|---|---|
| Gandhi | 450,000 | |||
| Mandela | 150,000 | |||
| Gbowee | 600,000 | |||
| Total |
8.
In this country there is one representative for every 75,000 residents.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
|---|---|---|---|---|
| Johnson | 225,000 | |||
| Rivera | 450,000 | |||
| Milk | 750,000 | |||
| Total |
9.
In this country there is one representative for every 40,000 residents.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
|---|---|---|---|---|
| Tamez | 280,000 | |||
| Teters | 200,000 | |||
| Herrington | 400,000 | |||
| Osawa | 360,000 | |||
| Total |
10.
In this country there is one representative for every 60,000 residents.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
|---|---|---|---|---|
| Johnson | 120,000 | |||
| Jackson | 480,000 | |||
| Cox | 720,000 | |||
| Browne | 420,000 | |||
| Total |
Exercise Group.
In each fictional country in problems 11-14, use the rules of the U.S. government (assume that all of a state’s electoral votes go to the candidate who received the majority of the votes in that state) to complete the table and determine the following:
The winner of the popular vote in the country and the percentage of votes they won.
The winner of the electoral college who becomes the president and the percentage of electoral votes they won.
11.
In this country from problem 7, there is one representative for every 50,000 residents.
| State | Votes for Candidate A |
Votes for Candidate B |
Number of Electoral Votes for A |
Number of Electoral Votes for B |
|---|---|---|---|---|
| Gandhi | 216,000 | 234,000 | ||
| Mandela | 37,500 | 112,500 | ||
| Gbowee | 489,450 | 110,550 | ||
| Total Votes |
12.
In this country from problem 8, there is one representative for every 75,000 residents.
| State | Votes for Candidate A |
Votes for Candidate B |
Number of Electoral Votes for A |
Number of Electoral Votes for B |
|---|---|---|---|---|
| Johnson | 115,650 | 109,350 | ||
| Rivera | 235,800 | 214,200 | ||
| Milk | 117,750 | 632,250 | ||
| Total |
13.
In this country from problem 9, there is one representative for every 40,000 residents.
| State | Votes for Candidate A |
Votes for Candidate B |
Number of Electoral Votes for A |
Number of Electoral Votes for B |
|---|---|---|---|---|
| Tamez | 95,480 | 184,250 | ||
| Teters | 104,200 | 95,800 | ||
| Herrington | 203,600 | 196,400 | ||
| Osawa | 46,080 | 313,920 | ||
| Total Votes |
14.
In this country from problem 10, there is one representative for every 60,000 residents.
| State | Votes for Candidate A |
Votes for Candidate B |
Number of Electoral Votes for A |
Number of Electoral Votes for B |
|---|---|---|---|---|
| Johnson | 52,440 | 67,560 | ||
| Jackson | 418,080 | 61,920 | ||
| Cox | 319,680 | 400,320 | ||
| Browne | 350,280 | 69,270 | ||
| Total Votes |
Exercise Group.
In each fictional country in problems 15-18, use the rules of the U.S. government to complete the table and determine the following:
The state that has the most electoral power
The state that has the least electoral power
15.
In this country from problem 7, there is one representative for every 50,000 residents.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
Electoral Votes per 50,000 people |
|---|---|---|---|---|---|
| Gandhi | 450,000 | ||||
| Mandela | 150,000 | ||||
| Gbowee | 600,000 |
16.
In this country from problem 8, there is one representative for every 75,000 residents.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
Electoral Votes per 50,000 people |
|---|---|---|---|---|---|
| Johnson | 225,000 | ||||
| Rivera | 450,000 | ||||
| Milk | 750,000 |
17.
In this country from problem 9, there is one representative for every 40,000 residents.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
Electoral Votes per 50,000 people |
|---|---|---|---|---|---|
| Tamez | 280,000 | ||||
| Teters | 200,000 | ||||
| Herrington | 400,000 | ||||
| Osawa | 360,000 |
18.
In this country from problem 10, there is one representative for every 60,000 residents.
| State | Population | Number of Representatives |
Number of Senators |
Number of Electors |
Electoral Votes per 50,000 people |
|---|---|---|---|---|---|
| Johnson | 120,000 | ||||
| Jackson | 480,000 | ||||
| Cox | 720,000 | ||||
| Browne | 420,000 |
19.
For the country in problem 7, determine all the possible combinations of states that would win the electoral college. What is the minimum number of votes needed to win the electoral college?
20.
For the country in problem 8, determine all the possible combinations of states that would win the electoral college. What is the minimum number of votes needed to win the electoral college?
21.
For the country in problem 9, determine all the possible combinations of states that would win the electoral college. What is the minimum number of votes needed to win the electoral college?
22.
For the country in problem 10, determine all the possible combinations of states that would win the electoral college. What is the minimum number of votes needed to win the electoral college?