Skip to main content

Section 3.3 Worksheets for Spreadsheets and Interest

Worksheet 3.3.1 Preview Activity for Section 3.2 and Due at the beginning of class. 3.1
A4US

Personal Reflections.

1.
Do you use a budget? Why or why not?
2.
List some places in your finances where you might be able to save a few dollars or more per week or per month.

Simple Interest.

Definition: Interest is only earned (or paid) on the original amount.

Example: You invest $500 and you earn 6% interest every year for 5 years.

Table 3.3.1.
Year Interest Balance
Start $500
1
2
3
4
5

Compound Interest.

Definition: Interest is earned on the original amount and any interest added to the account.

Example: You invest $500 at a rate of 6% interest compounded yearly for 5 years.

Table 3.3.2.
Year Interest Balance
Start $500
1
2
3
4
5

3.

[Optional] If you are doing this worksheet online, do the tables from the previous page in a spreadsheet, and then copy and paste them below.

Using Spreadsheet Formulas for Compound Interest.

You will need to use Microsoft Excel or Google Sheets while work on this worksheet. You can use a computer, tablet or smart phone with the Google Sheets App.

Future Value Formula: =FV(rate, nper, pmt, [pv], [type])

Present Value Formula =PV(rate, nper, pmt, [fv], [type])

Inputs:

4.
rate=
5.
nper=
6.
pmt=
7.
[pv]=
8.
[fv]=
9.
[type]=

Example 1..

If you invest $500 at 6% interest, calculate the balance after 5 years for each compounding interval. Write the formula used and inputs in proper syntax.
10.
Simple Interest
11.
Compounded Yearly
12.
Compounded Quarterly
13.
Compounded Monthly
14.
Compounded Daily (365)
15.
Compounded Continuously

Compounding Continuously.

If we let the number of compounding periods go to infinity we get a base of e in our function.
\begin{equation*} A=Pe^{rt} \end{equation*}
=P*exp(rate*years)

Effective Rate.

The corresponding rate if compounded yearly. Used to compare different compounding options.

=effect(nominal rate, periods per year)

Example 2..

Write the formula used and the inputs in proper syntax. Answer each question with a complete sentence, including units.
16.
How much would you need to deposit in an account that pays 5.25% compounded monthly to have $20,000 in 20 years?
17.
You get an inheritance of $15,000 and you decide to put it in an account that pays 7.1% interest compounded continuously. How much would it be worth in 25 years?
18.
You decide to save your tax refund of $1000 in an account that pays 6.5% compounded quarterly. How much would you have in 15 years?
19.
You are shopping for savings accounts and you find one with a rate of 3.25% compounded monthly and one with a rate of 3.15% compounded daily. Find the effective rates to determine which account has a better rate.

.

This box will be given on the quiz and tests. The inputs are also given when you start typing in a spreadsheet. You do not need to memorize the formulas, just know how to use them.
Financial Formulas.

=P + P*rate*years

=FV(rate, nper, pmt, [pv], [type])

=PV(rate, nper, pmt, [fv], [type])

=P*exp(rate*years)

=effect(nominal rate, periods per year)

=PMT(rate, nper, pv, [fv], [type])

Worksheet 3.3.2 In Class Activity for Section 3.2 and Section 3.1
A4US

Group Activity

Use a spreadsheet on a Chromebook, smartphone, laptop or tablet to work on these problems. Write down the spreadsheet syntax to show your work.

For example: =FV(.05/12, 2*12, 0, 1000).

Answer each question in a complete sentence.

1.

Your uncle is giving you a simple interest loan of $500 for one year at 4% interest. What is the total amount you will owe him?

2.

You borrowed $1500 from another relative. She charged you 5% APR, compounded monthly. If you paid her back 2 years later, how much money did you give her?

3.

You got a bonus of $7,500 and you want to start a college fund for your child. You find an account paying 9.75% APR compounded quarterly. If your child just turned two years old, how much will you have when they turn 18? How much of that account balance is interest?

4.

Calculate how much you would have in problem 3 above if it was compounded continuously instead of quarterly.

5.

If you are considering a credit card with an APR of 27.49%, compounded daily, what annual rate are you effectively paying?

6.

How much would you need to deposit today to have one million dollars if you can find an account that pays 10% interest compounded daily for 50 years?

7. Challenge Problem.

Sage deposited $2498 into an account paying 7.05% APR, compounded quarterly. Dionne deposited $2994 into an account paying 5.19% APR, compounded monthly. How many years will it take for their balances to (nearly) match?

Make a spreadsheet with “Year” in Column A, and spreadsheet formulas for each person, using a cell reference for the year. Then you can copy the formula down using the fill-down feature.

Round-Robin Problems..

Choose two people from your group to travel together and two to stay. Use the space below to write your formula for each problem.
8.
You deposit $2000 in an account earning 3% interest compounded monthly. How much will you have in the account in 20 years? How much interest will you earn?
9.
Which is better? An account that earns 7.25% compounded quarterly or an account that earns 7.15% compounded daily? Give the effective rate for each account.
10.
How much would you need to deposit in an account now in order to have $6,000 in the account in 8 years? Assume the account earns 6% interest compounded monthly.
11.
You deposit $4,500 in an account that earns 3.5% interest compounded continuously. How much will you have in 15 years?
12.
A friend lends you $200 for a week, which you agree to repay with 5% one-time interest. How much will you have to repay?

Worksheet 3.3.3 Gracie's Budget
A4US

In this lab, you will create a budget spreadsheet to keep track of monthly income, expences, and savings, and you will use several spreadsheet functions and formulas.

1.

Create a new spreadsheet in Goolge Sheets, Microsoft Excel or Apple Numbers. This lab will refer to functions and formulas in Google sheets.

2.

Gracie wants to save for a summer vacation with her friends. She estimates that her vacation will cost $2000. Can she afford to go? To find out, she decides to buget her income and expenses for the spring semester to determine if she'll have enough money saved in order to go. Set up your spreadsheet so that it matches the picture below.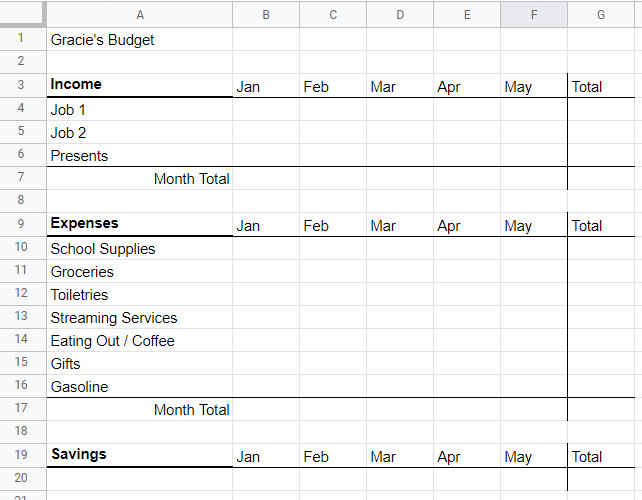

3.

Fill in the bugdget with the following information

  • Gracie's first job makes $500 a month.

  • Gracie only works her second job during March, April, and May. She makes $200 each of those months.

  • Gracie receives birthday money from some of her relatives in February totally $75.

  • Gracie pays for $35 of school supplies in January and $15 in March.

  • Gracie spends $100 a month on groceries.

  • Gracie spends $10 a month on toiletries (toothpaste, shampoo, etc.)

  • Gracie spends $25 a month on streaming services.

  • Gracie spends $70 a month on eating out and getting coffee.

  • Gracie spends $20 on birthday gifts for her family in the months of January (her mom), March (her brother), and May (her dad).

  • Gracie spends $45 on gasoline each month because she visits her family many weekends during the school year.

4.

Create formulas for the “Total” column, the “Month Total” rows, and the “Savings” row.

5.

You should end up computing Gracie's total savings as a number less than her goal of $2000. How much money does she save up in this scenario? How much is she short of her goal?

6.

Help Gracie decide what expenses to cut in order to reach her goal. Precisely list everything she should change, and what her new total savings will be after making your suggested changes.

7.

Copy and paste your spreadsheet into the space below.

8.

Use moral, ethical, and/or biblical reaons to explain why the changes you suggested above were the best choices for Gracie. Feel free to use your imagination to fill in necessary details about her life. Write 1-3 paragraphs.

This question will be graded according to your use of ethical, moral, or Biblical principles in your reasoning, and your use of numbers in your reasoning, such as:

  1. Interpretation: Ability to explain information presented in mathematical forms (e.g., equations, graphs, diagrams, tables, words)

  2. Application / Analysis: Ability to make judgments and draw appropriate conclusions based on the quantitative analysis of data, while recognizing the limits of this analysis

  3. Communication: Expressing quantitative evidence in support of the argument or purpose of the work (in terms of what evidence is used and how it is formatted, presented, and contextualized)