Skip to main content

Section 3.2 Interest

Worksheet 3.2.1 Credit Crunch Worksheet
A4US

When you use a credit card, you can pay off the entire balance at the end of the month and avoid paying any interest. If you do not pay the full amount, you are borrowing money from the credit card company. This is called credit card debt. Many people in the United States are concerned about the amount of credit card debt for both individuals and for society in general. In this lesson, you will use skills and ideas from previous lessons to think about some issues related to credit cards. You may want to refer back to the previous lessons.

1.

According to the Federal Reserve System the total credit card debt carried by Americans as of March 2015 was 848.1 billion dollars. Write this number in standard notation in dollars and also in scientific notation.

You will use the following information from a credit card disclosure in the next few questions.

Annual Percentage Rate (APR) for Purchases

0.00% introductory APR for 6 months from the date of account opening. After that, your APR will be 10.99% to 23.99% based on your creditworthiness. This APR will vary with the market based on the Prime Rate.

2.

APR stands for Annual Percentage Rate. It is the total interest rate for the entire year. However, we normally make a credit card payment each month. The amount of interest paid each month is called the Periodic Rate. Find the monthly Periodic Rate for an APR of 10.99%, rounded to two decimal places.

Creditworthiness is measured by a “credit score,” with a high credit score indicating good credit. In the following questions, you will explore how your credit score can affect how much you have to pay in order to borrow money. Juanita and Brian both have a credit card with the terms in the disclosure form given above. They have both had their credit cards for more than 6 months.

3.

Juanita has good credit and gets the lowest interest rate possible for this card. She is not able to pay off her balance each month, so she pays interest. Estimate how much interest Juanita would pay in the month of January if her unpaid balance is $5000. She has already owned the card for more than six months.

4.

If Juanita maintains an average balance of $5000 every month for a year, estimate how much interest she will pay in a year.

5.

Brian has a very low credit score and has to pay the highest interest rate. He is not able to pay off his balance each month, so he pays interest. Calculate how much interest he would pay in the month of January if his balance is $5000, to the nearest cent.

6.

If Brian maintains an average balance of $5000 every month for a year, calculate how much interest he will pay in a year.

You will use the following information from the disclosure for the next question. A cash advance is when you use your credit card to get cash instead of using it to make a purchase.

Table 3.2.1.

Annual Percentage Rate (APR) for Purchases

APR for Cash Advances

After that, your APR will be 10.99% to 23.99% based on your creditworthiness. This APR will vary with the market based on the Prime Rate.

28.99%. This APR will vary with the market based on the Prime Rate.

7.

Determine how to fill in the blank to create a reasonable statement.
Jeff pays the highest interest rate for purchases. Over a year, for a cash advance he would pay $ more interest for each dollar he charges to his card, compared to using it for a purchase.

8.

Determine how to fill in the blank to create a reasonable statement.
Lois pays the lowest interest rate for purchases. If she purchased a $400 TV using a cash advance, she would pay about times as much interest as she would if she used the card as a regular purchase.

Brian used a spreadsheet to record his credit card charges for a month. In a spreadsheet, you can refer to a "cell" (one of the boxes that hold numbers or words) using it's location. For example, $56.08 is in column B and row 2, so we say it is in cell B2.

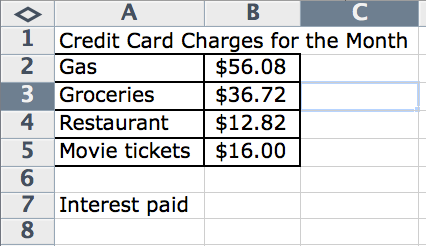
Brian entered the following formula in cell B7 to calculate his interest for these charges for one month.

= (0.2399/12) * (B2 + B3 + B4 + B5)

9.

Which of the following statements best explains what the expression means in terms of the context?

  • Brian found the interest charge for the month by dividing 0.2399 by 12 and multiplying it by the sum of Column B.

  • Brian added his individual charges. Then he divided 0.2399 by 12. Then he multiplied the two numbers.

  • Brian found the periodic rate by dividing his APR of 0.2399 by 12 months. He then added the individual charges to get the total amount charged to the credit card. He multiplied the periodic rate by the total charges to find the interest charge for the month.

10.

Which of the following are other ways that Brian could have done the calculation (there may be more than one correct answer)

  • = B2 + B3 + B4 + B5 * 0.2399 / 12

  • = (1/12)*0.2399*(B2 + B3 + B4 + B5)

  • = B2*0.2399/12 + B3*0.2399/12 + B4*0.2399/12 + B5*0.2399/12

  • = (B2 + B3 + B4 + B5)*0.2399/12

  • = (0.2399*(B2 + B3 + B4 + B5))/12

  • = (0.2399/12)*B2 + B3 + B4 + B5

Worksheet 3.2.2 Investment Lab
A4US

Sal, Cal and Val are triplets. Sal gets a paper route at age 14 and decides to invest $2000 at the beginning of each year in a mutual fund which averages a 10% annual return. Sal only makes deposits for 5 years and then leaves the balance to compound until retirement at age 65. Cal is impressed by Sal’s bank account, gets a job in college at age 19 and dutifully makes deposits into the same mutual fund for 8 years and then leaves the balance to compound until retirement at age 65. Val partied a lot growing up, but then gets a good job at the age of 27 and diligently makes deposits all the way to retirement at the age of 65. Your job in this project is to recreate the picture of the spreadsheet below in your own spreadsheet and answer the following questions:

Spreadsheet Template 11 

1.

(6 points) Before trying to recreate the spreadsheet below let's check that you understand where the numbers came from. Consider the cell C5, which shows $4,620. Write the mathematical equation whose answer is $4620. Then write the same equation replacing numbers with cell names whenever possible.
Hint.
Remember to replace the rate “10%” with I3, or even better, $I$3. The dollar signs will let you copy formulas better.

2.

(20 points) Consider the picture above. Recreate the spreadshee which tracks the growth of each person’s investment and extend it all the way down to age 65. You must take into account both the deposit and the growth rate of 10% each year. Remember to use “$I$3” instead of “10%” in your formulas.

If you are new to spreadsheets, feel free to check out this video Google Sheets Formula Tutorial 12 . For this lab you only need the first 4-5 minutes of this video.

3.

(12 points) For each person, calculate the total amount they deposited and the total interest they collected.

4.

(4 points) Change the annual interest rate to different numbers. Determine the interest rate where Sal and Val end with the same amount of money (rounded to the nearest tenth of a percentage point).

5.

(8 points) Using what you've learned in this lab, write a note to your friend explaining why it is financially wise to begin investing money as early as possible.

In order to get full credit for Exercise 2 you need to do two things.

  1. Show all your formulas by clicking View -> Show -> Formulas

  2. Turn your spreadsheet into a PDF by clicking File -> Download -> PDF (.pdf)

  3. This PDF that you just downloaded is the file you should submit with this lab, along with this worksheet. You will lose points if you don't follow directions.

docs.google.com/spreadsheets/d/1HN28mEYPbSk3LUHqK7RPtklRhb-4VZWRLuhQJndrgU0/edit?usp=sharing
youtu.be/9TVmdFtmbbo