Skip to main content

Worksheet 2.2.1 Credit Crunch Worksheet
A4US

When you use a credit card, you can pay off the entire balance at the end of the month and avoid paying any interest. If you do not pay the full amount, you are borrowing money from the credit card company. This is called credit card debt. Many people in the United States are concerned about the amount of credit card debt for both individuals and for society in general. In this lesson, you will use skills and ideas from previous lessons to think about some issues related to credit cards. You may want to refer back to the previous lessons.

1.

According to the Federal Reserve System the total credit card debt carried by Americans as of March 2015 was 848.1 billion dollars. Write this number in standard notation in dollars and also in scientific notation.
Solution.
These number can be written as $848,100,000,000 and as $\(8.481 \times 10^{11}\text{.}\)

You will use the following information from a credit card disclosure in the next few questions.

Annual Percentage Rate (APR) for Purchases

0.00% introductory APR for 6 months from the date of account opening. After that, your APR will be 10.99% to 23.99% based on your creditworthiness. This APR will vary with the market based on the Prime Rate.

2.

APR stands for Annual Percentage Rate. It is the total interest rate for the entire year. However, we normally make a credit card payment each month. The amount of interest paid each month is called the Periodic Rate. Find the monthly Periodic Rate for an APR of 10.99%, rounded to two decimal places.
Solution.
\(\frac{10.99}{12}\%=0.915833\% \approx 0.92\%\)

Creditworthiness is measured by a “credit score,” with a high credit score indicating good credit. In the following questions, you will explore how your credit score can affect how much you have to pay in order to borrow money. Juanita and Brian both have a credit card with the terms in the disclosure form given above. They have both had their credit cards for more than 6 months.

3.

Juanita has good credit and gets the lowest interest rate possible for this card. She is not able to pay off her balance each month, so she pays interest. Estimate how much interest Juanita would pay in the month of January if her unpaid balance is $5000. She has already owned the card for more than six months.
Solution.
Answers will vary. 0.92% is a little less than 1%, so the interest owed will be a little less than $50 (1% of 5,000)

4.

If Juanita maintains an average balance of $5000 every month for a year, estimate how much interest she will pay in a year.
Solution.
Answers will vary. A little less than about $600 (12 times $50)

5.

Brian has a very low credit score and has to pay the highest interest rate. He is not able to pay off his balance each month, so he pays interest. Calculate how much interest he would pay in the month of January if his balance is $5000, to the nearest cent.
Solution.
His Periodic Rate is 23.99/12 = 1.999167%. Multiply 0.01999167 times $5000 = $99.96. Note that it's important to keep a lot of decimal places in the periodic rate since that number is being multiplied by a large dollar amount.

6.

If Brian maintains an average balance of $5000 every month for a year, calculate how much interest he will pay in a year.
Solution.
Multiply $5000 times 0.2399 to get $1,199.50

You will use the following information from the disclosure for the next question. A cash advance is when you use your credit card to get cash instead of using it to make a purchase.

Table 2.2.1.

Annual Percentage Rate (APR) for Purchases

APR for Cash Advances

After that, your APR will be 10.99% to 23.99% based on your creditworthiness. This APR will vary with the market based on the Prime Rate.

28.99%. This APR will vary with the market based on the Prime Rate.

7.

Determine how to fill in the blank to create a reasonable statement.
Jeff pays the highest interest rate for purchases. Over a year, for a cash advance he would pay $ more interest for each dollar he charges to his card, compared to using it for a purchase.
Solution.
For a cash advance, he would pay 28.99%, or $0.2899 per dollar. For a purchase, he would pay 23.99%, or $0.2399 per dollar. With the cash advance, he would pay $0.2899-$0.2399 = $0.05 more interest for each dollar he charges.

8.

Determine how to fill in the blank to create a reasonable statement.
Lois pays the lowest interest rate for purchases. If she purchased a $400 TV using a cash advance, she would pay about times as much interest as she would if she used the card as a regular purchase.
Solution.
For a cash advance, she would pay 28.99%. For a purchase, she would pay 10.99%. The cash advance interest rate is 28.99/10.99 = 2.64, or about two-and-a-half times as much interest as the purchase rate.

Brian used a spreadsheet to record his credit card charges for a month. In a spreadsheet, you can refer to a "cell" (one of the boxes that hold numbers or words) using it's location. For example, $56.08 is in column B and row 2, so we say it is in cell B2.

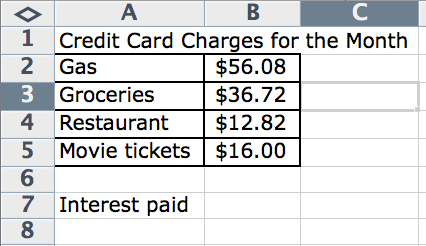
Brian entered the following formula in cell B7 to calculate his interest for these charges for one month.

= (0.2399/12) * (B2 + B3 + B4 + B5)

9.

Which of the following statements best explains what the expression means in terms of the context?

  • Brian found the interest charge for the month by dividing 0.2399 by 12 and multiplying it by the sum of Column B.

  • Brian added his individual charges. Then he divided 0.2399 by 12. Then he multiplied the two numbers.

  • Brian found the periodic rate by dividing his APR of 0.2399 by 12 months. He then added the individual charges to get the total amount charged to the credit card. He multiplied the periodic rate by the total charges to find the interest charge for the month.

Solution.
While all the options describe the calculations, the one that describes the expression the best in terms of the context is: Brian found the periodic rate by dividing his APR of 0.2399 by 12 months. He then added the individual charges to get the total amount charged to the credit card. He multiplied the periodic rate by the total charges to find the interest charge for the month.

10.

Which of the following are other ways that Brian could have done the calculation (there may be more than one correct answer)

  • = B2 + B3 + B4 + B5 * 0.2399 / 12

  • = (1/12)*0.2399*(B2 + B3 + B4 + B5)

  • = B2*0.2399/12 + B3*0.2399/12 + B4*0.2399/12 + B5*0.2399/12

  • = (B2 + B3 + B4 + B5)*0.2399/12

  • = (0.2399*(B2 + B3 + B4 + B5))/12

  • = (0.2399/12)*B2 + B3 + B4 + B5

Solution.
Most of these are equivalent to the original calculation. The two that are not are missing parentheses necessary due to order of operations. For example, in the expression "= (0.2399/12)*B2 + B3 + B4 + B5", only the first charge is getting multiplied by the periodic rate. To make this correct, we would need to add grouping symbols to first sum the charges: = (0.2399/12)*(B2 + B3 + B4 + B5)