Worksheet Problem Situation: How Big is a Billion?
A large economic and political concern is the federal deficit, the amount of money spent by the federal government in excess of revenue collected annually. The federal budget deficit for 2015 was approximately $435 billion. The federal debt is the accumulated deficits from all years, and in 2015 was about $18.1 trillion.
It is difficult to understand just how big a billion or a trillion is. Here is a way to help you think about it.
| 1 million | = 1,000 \(\times\) 1,000 | = 1,000,000 | \(=10^6\) |
| 1 billion | = 1,000 \(\times\) 1,000 \(\times\) 1,000 | = 1,000,000,000 | \(=10^9\) |
| 1 trillion | = 1,000 \(\times\) 1,000 \(\times\) 1,000 \(\times\) 1,000 | = 1,000,000,000,000 | \(=10^{12}\) |
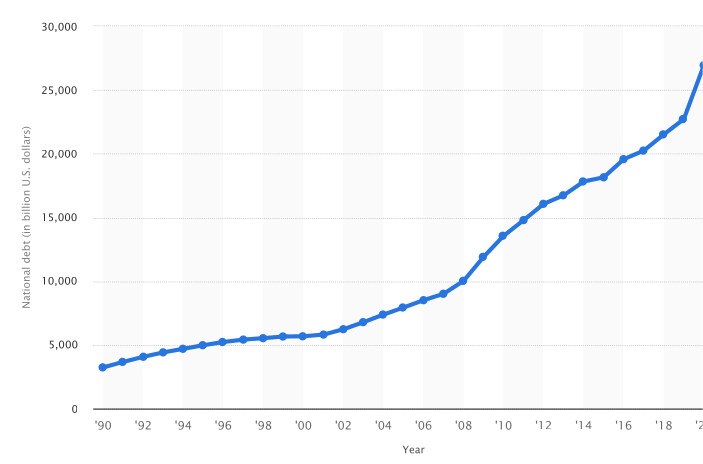
National Debt.
1.
What is a simpler way to express 2000 billion dollars?2.
Imagine a stack of 1,000 one‐dollar bills, which is about 4.3 inches tall. Imagine combining 1,000 stacks of 1,000 one‐dollar bills. How much money is in the stack?3.
How tall would that stack be, in inches? How tall in feet (rounded to the nearest foot)National Debt continued.
4.
Now imagine combining 1000 stacks like the one above in exercise Worksheet Exercise 2.2.2. How much money is in the stack?5.
How tall would that stack be, in feet? How tall would that stack be, in miles? (Round to the nearest mile)6.
Now imagine combining 1000 stacks like the one in exercise Worksheet Exercise 2.2.4. . How much money is in the stack?7.
How tall would that stack be, in miles?Problem Situation 2: Scientific Notation.
You saw that 1 billion can be written as 1,000,000,000 or represented as \(10^9\text{.}\) How would 2 billion be represented? Since 2 billion is 2 times 1 billion, then 2 billion can be written as \(2 \times 10^9\text{.}\) Writing numbers in this way is called scientific notation. Scientific notation is used primarily for writing very large numbers and very small numbers. In this lesson, we will focus on large numbers.
The form for scientific notation is \(M \times 10^n\) where \(1\leq M < 10\text{.}\) The exponent equals the number of decimal places between the location of the decimal in the number as written in standard notation and the number written in scientific notation.
For example, if the number 500 were to be written in scientific notation, it could be thought of as \(5 \times 100\) or \(5 \times 10 \times 10\) which is equal to \(5 \times 10^2\text{.}\) The decimal point has been moved 2 places which corresponds to the exponent of 2.
Likewise, if the number 4300 were to be written in scientific notation, it could be thought of as \(4.3 \times 1000\) or \(4.3 \times 10 \times 10 \times 10\) which is equal to \(4.3 \times 10^3\text{.}\) The decimal point has been moved 3 places (between 4300. and 4.3) which corresponds to the exponent of 3.
8.
Write the numbers below in both standard notation and scientific notation.| Words | Standard Notation | Scientific Notation |
| four hundred |
\(\hspace{2in}\) |
\(\hspace{2in}\) |
| twenty three thousand |
|
|
| 7.2 million |
|
|
9.
The table below contains the national deficit and national debt for various years. Write the number in both standard notation and scientific notation.| Words | Standard Notation | Scientific Notation |
| 1965 deficit: $1.41 billion |
\(\hspace{2in}\) |
\(\hspace{2in}\) |
| 2009 deficit: $1412.69 billion |
|
|
| 2014 deficit: $484.6 billion |
|
|
| 2014 debt: $18.2 trillion |
|
|
Problem Situation 3: Comparing the Sizes of Numbers.
One of the skills you will learn in this course is how to write quantitative information. A writing principle that you will use throughout the course is given below followed by Question 2, which gives you an example of how to use this principle.
Writing Principle: Use specific and complete information. The reader should understand what you are trying to say even if they have not read the question or writing prompt. This includes
information about context, and
quantitative information
10.
A headline in 2014 10 read “Scott vetoes $69 million in $77-billion state budget”. Is the $69 million a small or large portion of the total state budget? The following four statements are all correct. Which statement provides the best description, based on the writing principle?The portion vetoed is a very small part of the entire state budget
$69 million is about a thousandth of $77 billion
The $69 million vetoed is a very small part of the entire state budget of $77 billion
The $69 million that was vetoed is about one tenth of one percent of the total $77 billion state budget.
11.
The federal budget in 2012 included $471 billion for Medicare and $47 billion for International Affairs. Complete the statement below that compares the two quantities.The budget of $471 billion for Medicare is about times larger than the $47 billion budget for International Affairs.
12.
Using the writing principle above, in a full sentence compare the 2009 deficit and the 2014 deficit from exercise Worksheet Exercise 2.2.9Estimate.
13.
About 3 million working people in the U.S. make at or below the federal minimum wage of $7.25 per hour. Estimate the amount of money needed per year to raise their wages to $15 per hour.14.
The amount of money needed to buy everyone in the United States a box of Girl Scout cookies.15.
The amount of money needed to send all adults in your state to college for four years.16.
If the U.S. national debt was $22 trillion in 2019, and was evenly divided among the people living in the United States, how much would each person's share be?Calculate.
17.
About 3 million working people in the U.S. make at or below the federal minimum wage of $7.25 per hour. Estimate the amount of money needed per year to raise their wages to $15 per hour.18.
The amount of money needed to buy everyone in the United States a box of Girl Scout cookies.Calculate (continued).
19.
The amount of money needed to send all adults in your state to college for four years.20.
If the U.S. national debt was $22 trillion in 2019, and was evenly divided among the people living in the United States, how much would each person's share be?Percent of National Debt.
21.
If the U.S. budget is about $4.1 trillion, estimate the percentage of the budget which would be needed to pay for your estimate in Question 5 above.22.
If the U.S. budget is about $4.1 trillion, calculate the percentage of the budget which would be needed to pay for your estimate in Question 9 above. Round to the nearest hundredth of a percent.Fast Food Restaurant Budget.
| A | B | C | D | E | F | G | |
| 1 | Employees\(\hspace{.25 in}\) | Av. hours\(\hspace{.25 in}\) | Wages ($ per hour) | Total Labor Cost | Overhead\(\hspace{.75 in}\) | Revenue\(\hspace{.75 in}\) | Profit.\(\hspace{1 in}\) |
| 2 |
|